Escucha el podcast aquí:
Los amigos de La Camarilla me invitaron a participar en su podcast sobre cine. Hablamos un rato sobre cine, matemáticas y cosas del pueblo. Aquí os dejo un resumen de lo que se habló en la hoguera bajo una intensa fogata.
Como ellos mismo de describen La Camarilla es un podcast de entretenimiento, cine y humor absurdo. Videojuegos, música, la cultura pop expuesta de una manera sencilla y amena. Rita, Lito, Drolo, Taker y Doctor Linxi te traen desde diversas zonas de la geografía española un programa cargado de sorpresas, entrevistas inesperadas y pasión.
Unas preguntas para calentar
- ¿Eres matemático y estadístico no? Cuéntanos un poco por qué elegiste ese campo.
Eso parece decir un título. Tengo que reconocer que de pequeño no era para nada lo que se esperaba de un futuro matemático, de hecho mi único suspenso en el colegio fue en un examen de cálculo, que me harte de llorar. Pero luego, llegando el momento, siempre me ha gustado aprender y entender lo que me rodea y entendí que la mejor forma de hacerlo era a través de la matemática y la estadística, y hasta hoy. Además, siempre me han gustado los retos y hasta el momento no conozco otro más cmplejo que interactuar con las matemáticas.
- ¿Y escritor también no?
Esa es buena. De escritor tengo lo que Abel de delantero centro (sin ofender). Pero es cierto que cuando estoy inspirado o cuando la chiquilla con la que me estoy viendo me deja suelo escribir algún que otro texto y los publico por redes sociales. Además, mi padre me suele meter caña y me corrige los textos y yo a él, que escribe muy bien aunque no publica, y así vamos.
- ¿Actualmente a qué te dedicas?
Sigo estudiando en la Facultad de Matemáticas de Sevilla, buscando un poco cómo encaminar los próximos años de mi vida y elegir un tema para el doctorado. Actualemente investigo sobre Aprendizaje con Refuerzo Profundo (un tema muy de moda) que es parte del campo de la Inteligencia Artificial, pero me gusta también el análisis de datos y la teoría que hay detrás de la toma de decisiones.
- ¿Y esa relación del cine con las matemáticas?
Quizás no tanto como vosotros, que sois prácticamente unos técnicos en la materia, pero también soy un gran aficionado al cine. Me he tragado desde “Un tranvía llamado deseo” hasta “Parásitos” pasando por “Lo llamaban Trinidad”. Tanto es el interés, que en parte, en mi Trabajo de Fin de Grado trato de entender que fue lo que se me escapó la primera vez que vi “Una Mente Maravillosa”
- Tienes una web ¿no? Para que los oyentes puedan seguir un poco tus publicaciones o escribirte burradas sobre la turra que les has dado en el programa de hoy.
Un poco de publicidad, mi web es https://torrejonvalenzuela.com/. Este verano me decidí aventurarme a escribir una web soporte que las suelen llamar: conforme vas aprendiendo escribes un post sobre ello y así lo asimilas mejor. Tiene poco tiempo de vida y al final tiene más de web personal que web soporte, publico ahí más poemas que cosas de mis estudios, pero bueno, ahí está poco a poco cogiendo forma. El siguiente post es sobre La Camarilla asegurado.
- ¿Qué te parece La Camarilla?
La Camarilla es un buen programa para ponertelo de fondo y asentir a veces cuando escuchas algo con lo que estas de acuerdo, que me suele pasar. Sois amenos, de risas, pero cuando hay que ponerse serios lo hacéis, sin ir más lejos con lo de Parásitos revisasteis prácticamente la historia de la división de Corea y su historia posterior. Además, creo que todo el mundo debería de escucharlo, al contrario que con las matemáticas, el cine le suele gustar a todo el mundo y las películas sobre las que habláis son muy modernas, que seguro que las han visto.
La parte sustanciosa de la entrevista
Yo suelo ser una persona que duda mucho cuando tiene que tomar una decisión, casi siempre por el miedo a equivocarse. Tanto es que os puedo contar algo que me ocurre el 78% de las veces que tengo que tomar una decisión:
Un campesino alimentaba todos los días a su asno con dos sacos de heno, uno más grande que el otro. El asno siempre escogía el saco más grande de los dos. Un día el campesino le proporcionó dos sacos iguales y el asno, acostumbrado a saber que saco escoger siempre, no supo tomar un decisión clara y acabó desfalleciendo.
Claramente, es una broma, pero esta paradoja, que os la he colado en el podcast, lo que pone de relieve es otro problema dentro de la toma de decisiones, si siempre tomamos decisiones bajo unos supuestos débiles, cuando haya que enfrentarse a decisiones más complejas el panorama se complica.
Estos son solo algunos de los problemas que se pueden presentar, por eso no parece mala opción tener herramientas para poder tomar buenas decisiones y aquí las matemáticas y las estadísticas son buenas aliadas. Por poner algunos ejemplos y asociarlos al cine están:
- Teoría de Juegos \(\rightarrow\) Una mente maravillosa.
- Análisis de datos \(\rightarrow\) Moneyball.
- Teoría de la probabilidad \(\rightarrow\) 21 BlackJack.
Una mente maravillosa
La película, ya que sé que os gustan los aspectos más cinematográficos, empieza con una de las mejores bandas sonoras desde mi punto de vista de James Horner y hace, en el primer minuto, una referencia rotunda a un momento histórico: “Los matemáticos ganaron la guerra”. Como buenos cinéfilos, ¿en qué otra película se explica cómo?1.
La parte más matemática queda latente en la primera parte de la película. John Nash, el protagonista, es un gran matemático que compite con sus compañeros para que se le adjudique un programa de financiación para sus investigaciones, aunque él en ese momento desconozca el tema de su doctorado. Tal es la competencia, en una de las escenas le invitan a jugar al Go (juego que tiene lo suyo y para el que hay un documental en Netflix) y no acepta la derrota. Es ahí cuando empiezan las primeras referencias a lo que se conoce como Teoría de Juegos: juego imperfecto, juego dinámico, etc.
Antes de entrar a analizar algunas escenas, creo que es bueno que os introduzca un poco que se entiende por Teoría de Juegos. ¿Qué creéis? ¿Sobre cómo jugar al FIFA?
La Teoría de Juegos no es más que el análisis de conflictos (juegos) y la búsqueda de una estrategia óptima para resolver ese conflicto. Importante, se supone que los individuos son racionales e inteligentes: los competidores buscan obtener el máximo beneficio. Existen diversas formas de distinguir o clasificar los juegos, siendo las principales:
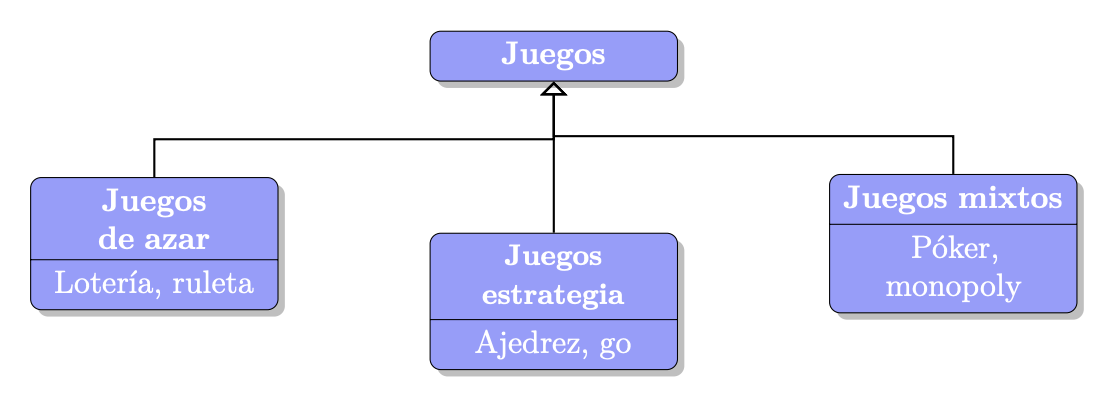
- Juegos no cooperativos vs juegos cooperativos.
- Juegos estratégicos (las jugadas se presentan en el mismo tiempo, piedra-papel-tijeras) vs juegos dinámicos (el orden de los turnos de jugada es relevante, póker). Dentro de los juegos dinámicos se puede tener información perfecta (ajedrez) o imperfecta (póker) según si se conocen las acciones previas de los jugadores o no.
- Juego de suma cero (el beneificio de un jugador es la pérdida del otro, ajedrez ó póker) vs de suma no nula (dilema del prisionero).
Por ejemplo, cuando pierde la partida de Go, se dice que es porque el juego tiene que ser imperfecto. Hay otra escena en la que aparecen ciertos dibujos en la ventana de la biblioteca y el dice que son un grupo jugando al fútbol, palomas luchando por unas migas de pan y una mujer persiguiendo al hombre que le robó el bolso. Todos estos son ejemplos de “conflictos” o “juegos”. ¿Creéis que en estos juegos importa el turno de cada jugador o es irrelevante? Importa, se tratan de juegos dinámicos, no es lo mismo que empieces a correr antes de que te roben el bolso que después.
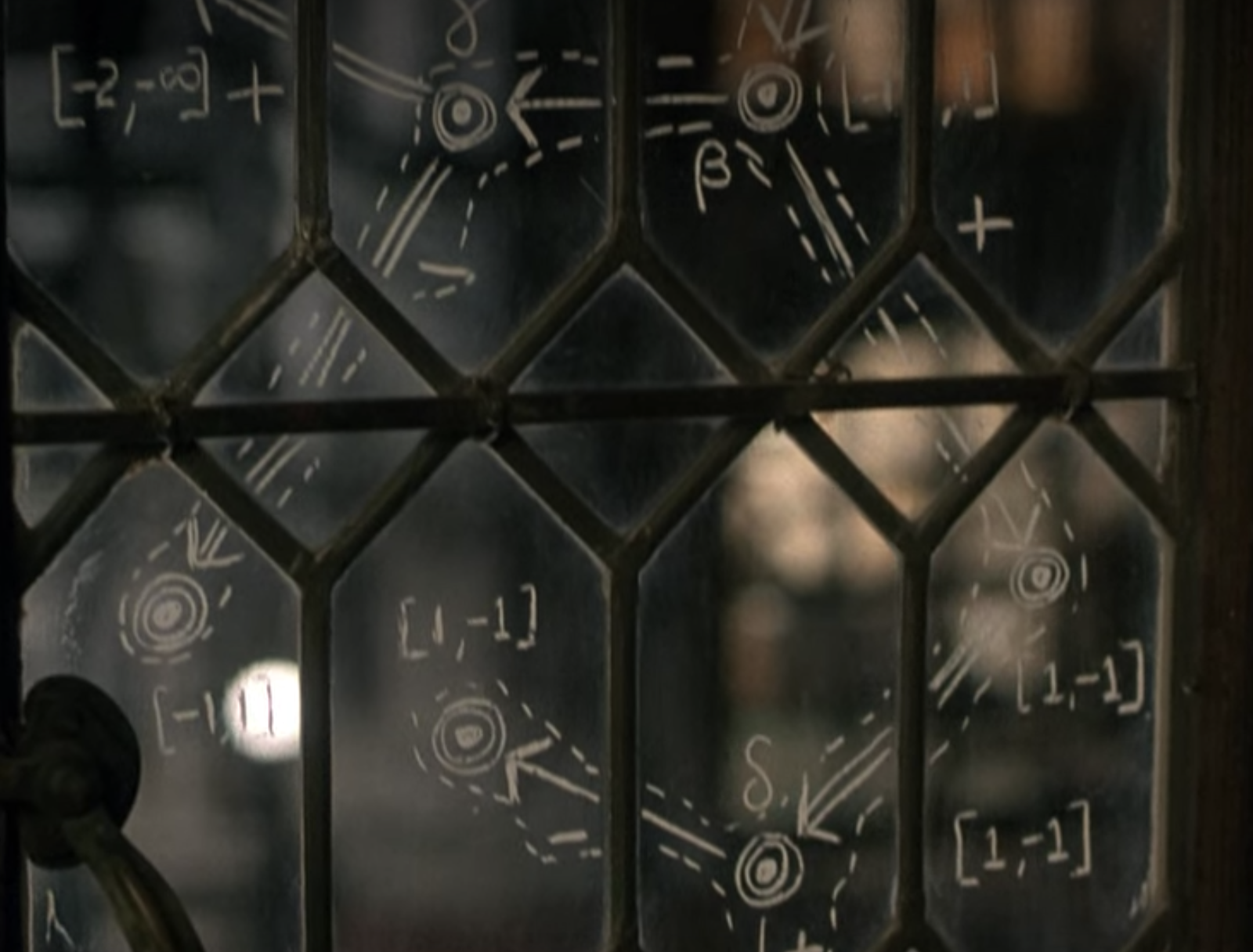
En esa misma escena, Nash, o el personaje en la película, dice:
“En toda competición siempre pierde alguien, […] si encontrase una ecuación de equilibrio donde no predominase ningún hecho concreto y no perdiera nadie, te imaginas…”
Con esto se refiere a lo que se denomina precisamente equilibrio de Nash. Si hay un conjunto de estrategias tal que ningún jugador se beneficia cambiando su estrategia mientras los otros no cambien la suya, entonces ese conjunto de estrategias y las ganancias correspondientes constituyen un equilibrio de Nash. Con un razonamiento puramente matemático, el jugador elige su mejor opción, que trata de ser una anticipación a lo que harán los demás jugadores. Para entender este concepto vamos a jugar:
Supongamos que somos un conductor y vamos conduciendo por una carretera muy estrecha a toda pastilla. De cara se nos acerca otro conductor a toda pastilla también. Mis únicas opciones son tirarme a la derecha o a la izquierda y las mismas para el otro conductor. ¿Qué haríais?
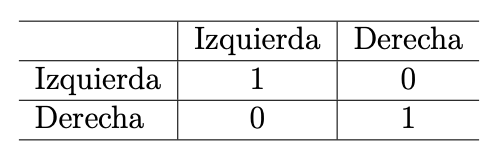
La intuición es tirarnos a la derecha, ¿pero tenemos certeza de que el otro jugador se tirará a su derecha? Los equilibrios de Nash de este juego serían ambos caer a la derecha, ambos a la izquierda y el más importante quizás, aleatorizar con probabilidad 1/2 tirarme a la derecha o la izquierda. Con esta última forma de jugar se demuestra que siempre voy a poder jugar a todo juego de forma que no pierda nadie (OJO, no de forma que ganemos todos) porque en promedio obtendré un beneficio para los dos.
Otra escena curiosa es la que aparece justo después. Una mujer se fija en él y su amigo le pide que vaya. Entonces dice:
“Caballeros, debo recordarles que mis probabilidades de éxito aumentan en cada nuevo intento,…”
¿Es cierto? En general no, por ejemplo si jugamos muchas veces a la lotería lo más probable es que acabemos arruinándonos que ganando. En esa frase entiendo que hace referencia a los juegos repetidos y al concepto de aprender en juegos. Jugar de forma repetida al juego de ligar en este caso. Una vez que nos hemos llevado el primer desamor o la primera cobra, se supone que adquirimos nueva información sobre el juego que podemos aplicar la siguiente vez que juguemos.
La última escena que quiero analizar con vosotros es la que considero la mejor de la película. Aparece Nash, agobiado porque no ve salida a su idea, y llegan los amigos con ganas de cerveza. En ese momento entra en escena una mujer guapísima y su grupo de amigas y todos se quedan perplejos fijándose solo en ella. Es cuando lo ve claro (dramatizanción de la película claro). Las teorías económicas de Adam Smith en adelante dicen que para poder obtener el mayor beneficio cada jugador tiene que ser egoísta y pensar en su propio bienestar. Sin embargo, si todo el mundo va en busca de la más guapa, se obstaculizan y ninguno de ellos consigue ligar con ella. Es entonces cuando van en busca del resto de amigas y estas pasan de ellos porque a nadie le gusta ser segundo plato. Para evitarlo, él propone que vayan directamente a por las amigas, cada uno por una, obviando a la más guapa, de esta forma ninguno gana lo mejor pero ninguno sale perdiendo. Esto es lo que comentaba antes que en el equilibrio de Nash se busca que nadie salga perdiendo, no que todos ganen.
Esto son los 30 primeros minutos de película. En el resto de la película se habla de su vida personal, la eskizofrenia que padecía, etcétera. Aunque no hablaremos mucho más de ello para no destripar el interés de la película. Esto se va intercalando con algunas escenas con matemáticas de fondo y quizás la más interesante es cuando está exponiendo sus resultados sobre la Hipótesis de Riemann, que es uno de los problemas que si consigues resolver pueden hacerte rico.
Al final de la película, en su discurso de aceptación del premio Nobel, dice lo siguiente:
“He buscado a través de lo físico, lo metafísico, lo delirante,… y vuelta a empezar. Y he hecho el descubrimiento más importante de mi carrera, el más importante de mi vida. Sólo en las misteriosas ecuaciones del amor puede encontrarse alguna lógica”.
Si queréis entender la razón de estás palabras tendréis que ver la película. Yo aun sigo el la búsqueda de esas ecuaciones para intentar resolverlas, pero sé por experiencia que aquellos que han conseguido resolverlas son un poco más felices.
Moneyball
Esta es sin duda, hasta el momento, mi película favorita. Narra como Billy Beane y Paul de Podesta (en la película le cambian el nombre por Peter Brand) consiguen con un salario muy inferior al resto de equipos de la MLB transformar a los Oakland Athletics en un equipo competitivo de la liga de béisbol americana.
Imaginaros que queréis construir un equipo de fútbol o baloncesto en Los Barrios, que queremos estar a nivel del Cádiz, Betis o Sevilla pero tenemos como presupuesto lo que nos da nuestra abuela los fines de semana, ¿qué haríais?
Solución: Recurrir a las matemáticas. De hecho, en este caso, a la estadística para ser justos y exactos. Pues esto es justo lo que hicieron Billy y Paul para los Oakland Athletics.
En su caso emplearon los principios que años atrás personas como Bill James habían desdarrollado mientras se planteaban si el béisbol era un juego que se podía descrifrar con datos y estadística. Nace lo que se conoce hoy como la Sabermetría. Hoy en día este análisis se ha extendido al resto de deportes y está muy reconocido, pero en aquel entonces…
Antes de analizar algunos aspectos de la película sería bueno ver cómo se juega al béisbol, que es más complejo de lo que parece. Resumidamente, en el béisbol se juegan 9 entradas (innigs) por equipo:
- 1 turno bateo + 1 turno defensa \(\Rightarrow\) fin entrada.
- Si hay empate \(\Rightarrow\) entradas adicionales.
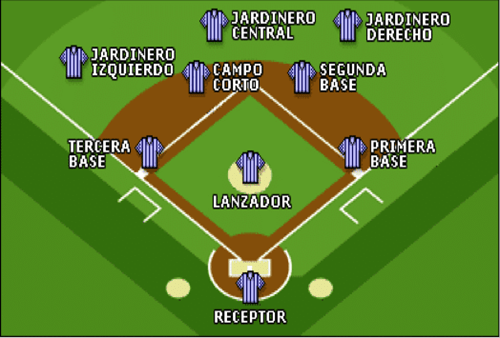
En un juego se enfrentan bateador vs defensa:
- Anotación de un punto: recorrer las 4 bases volviendo a home.
- Se avanza de base por bateo dentro del campo o por 3 bolas del lanzador.
- Un jugador por base.
- Si el bateo es HOME RUN \(\Rightarrow\) carrera del jugador y todos los que estén en bases.
- 3 bateadores eliminados \(\Rightarrow\) cambio turno
- Eliminar por: strike, bateo pero cogen la pelota o bateo pero te detienen.
Su objetivo era comprar jugadores que, a pesar de sus deficiencias físicas o defectos como edad, personalidad, etc., impulsaran carreras. Centrémosnos, por ejemplo, en las métricas para los bateadores. Tradicionalemente en el béisbol un jugador con un buen porcentaje en base o promedio de bateo se consideraba un buen bateador.
\[OBP = \frac{H+BB+HBP}{AB+BB+HBP+SF}\]
- \(H \equiv\) hits
- \(BB \equiv\) bolas por base
- \(HBP \equiv\) hit by pitch
- \(AB \equiv\) at bat
- \(SF \equiv\) sacrifice fly
El promedio de bateo mide cuantas veces el bateador conecta la bola, ¿qué problemas creéis que tiene esta métrica?2 Por eso se propuso como otra métrica para medir la validez de un bateador el slug.
\[SLG = \frac{1B + 2 \times 2B + 3 \times 3B + 4 \times HR}{AB}\]
- \(1B \equiv \#\) de singles
- \(2B \equiv \#\) de dobles
- \(3B \equiv \#\) de triples
- \(HR \equiv \#\) de homeruns
El slug valora que el jugador no sólo sea bueno en el bateo, sino que sea capaz de llegar a segunda, tercera o home, ponderando la importancia de estas. Actualmente se combinan tanto el promedio de bateo como el slug en la métrica OPS. Otra métrica muy empleada es la de runs batted in (carreras impulsadas). Así, incluyendo numerosas métricas de estos jugadores reducían el valor de estos a un sólo número que no tenía en cuenta otros defectos ni prejuicios que tenían los equipos de béisbol, como se dice en la película: “un equipo de patitos feos”. Pero el análisis no solo comprendía el estudio de los jugadores. También se analizaban le frecuencia y el lugar del campo en el que el bateador enemigo mandaba la pelota y en función de ello movían la defensa.
Todo esto está muy bien, pero al principio de la película se ve como el equipo parece no arrancar, ¿por qué? Bueno en parte porque el proyecto, innovador que nadie entendía hasta el momento, debía de serle explicado a los jugadores y equipo técnico. Los jugadores no eran contratados por mejorar su juego sino por hacer de la mejor forma aquello en los que ya eran buenos. La otra parte, y siento traer esto a colación, el tamaño sí importa. Al principio de temporada el tamaño de la muestra sobre la que basan sus cálculos es muy pequeña, con que las conclusiones están muy poco fundamentadas. Conforme la muestra va aumentando de tamaño, por la Ley de los Grandes Números, los resultados se van ajustando y pueden obtener conclusiones más realistas. Por este motivo el gran problema eran los playoffs, donde la muestra es muy pequeña y no cabe sitio para la mejora.
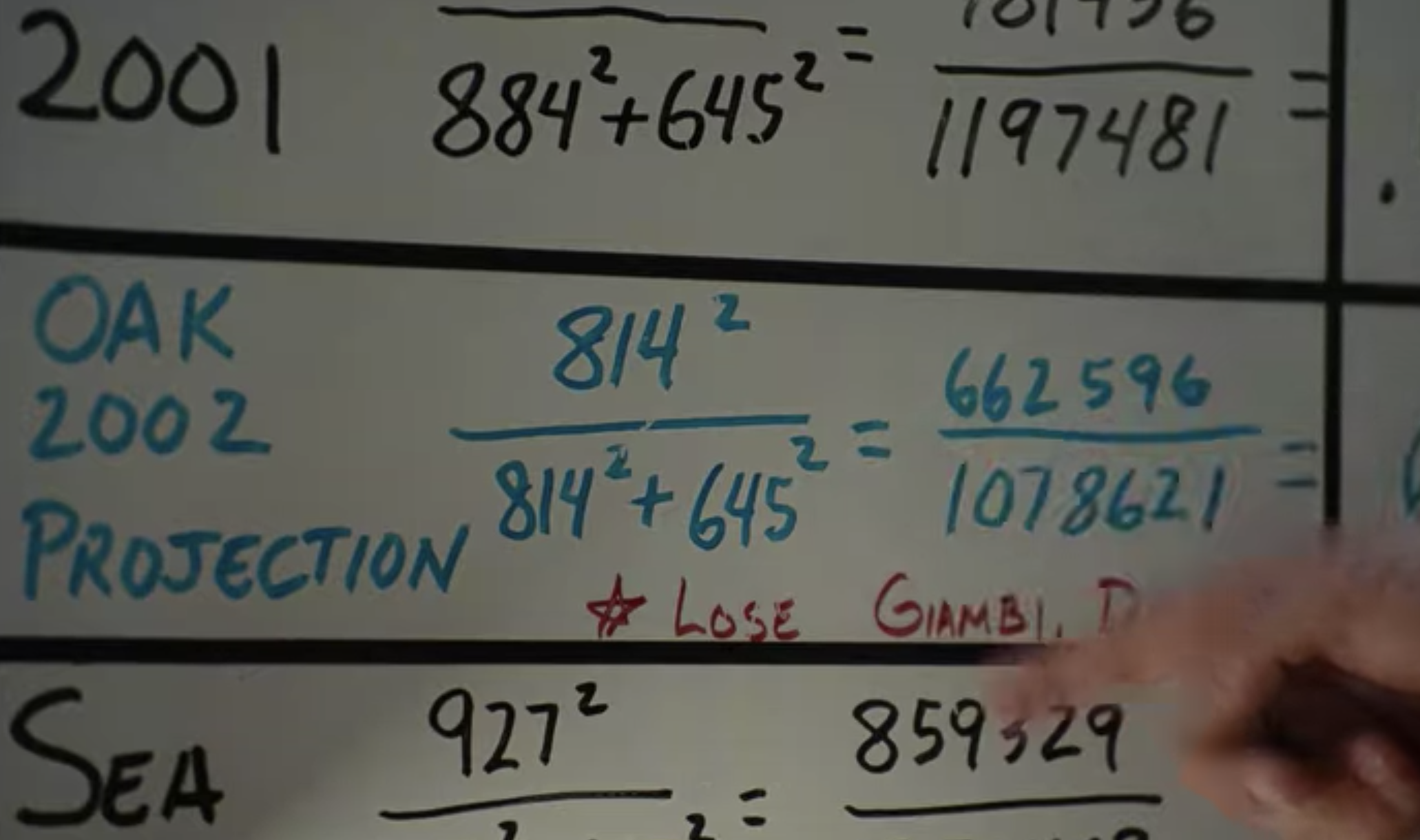
Actualmente este planteamiento se lleva al resto de deportes desde distintas perspectivas, no solo desde el análisis de jugadores, también para formar estrategias, analizar jugadas, predecir resultados, etc. Un ejemplo es el proyecto que los Houston Rockets, equipo de baloncesto de la NBA, tenían hasta la temporada pasada. Un estudio confirmó que los tiros más provechosos en el baloncesto eran triples y los tiros en los que se entraban a canasta, los tiros a media distancia eran los que menos. Con esto en mente, los Houston Rockets decidieron optar por jugadores que fuesen buenos en este cometido, que resultan ser jugadores de estatura menor a la media, small ball.
Al final de la película invitan a Billy Beane a convertirse en el General Manager de los Boston Red Sox, esto ocurrió en realidad como se cuenta en el libro homónimo MoneyBall de Michael Lewis, que recomiendo para aquel que empiece a interesarse poor el tema. Billy Beane termina declinando la oferta. Los Red Sox acabaron contratando a Bill James. Empezaba la revolución en el béisbol y en el deporte en general.
Billy Beane: “How can you not be romantic about baseball?”
21 BlackJack
La última película que intentamos destripar fue 21 BlackJack. Esta película es muy jugosa desde el punto de vista de la Teoría de la Probabilidad, ya que el juego del BlackJack es un juego totalmente aleatorio.
Problema de Monty Hall
En primer lugar, planteamos el conocido como Problema de Monty Hall
Supón que estás en un concurso, y se te ofrece escoger entre tres puertas: detrás de una de ellas hay un coche, y detrás de las otras, cabras. Escoges una puerta, digamos la nº1, y el presentador, que sabe lo que hay detrás de las puertas, abre otra, digamos la nº3, que contiene una cabra. Entonces te pregunta: “¿No prefieres escoger la nº2?”. ¿Es mejor para ti cambiar tu elección?
¿Que haríais?3
El BlackJack
La otra parte de la película que analizamos fue el blackjack.
El blackjack, también llamado veintiuno, es un juego de cartas, propio de los casinos con una o más barajas inglesas de 52 cartas sin los comodines, que consiste en sumar un valor lo más próximo a 21 pero sin pasarse. En un casino cada jugador de la mesa juega únicamente contra el crupier, intentando conseguir una mejor jugada que este. El crupier está sujeto a reglas fijas que le impiden tomar decisiones sobre el juego. Por ejemplo, está obligado a pedir carta siempre que su puntuación sume 16 o menos, y obligado a plantarse si suma 17 o más. Las cartas numéricas suman su valor, las figuras suman 10 y el As vale 11 o 1, a elección del jugador. En el caso del crupier, los Ases valen 11 mientras no se pase de 21, y 1 en caso contrario. La mejor jugada es conseguir 21 con solo dos cartas, esto es con un As más carta de valor 10. Esta jugada se conoce como Blackjack o 21 natural. Un Blackjack gana sobre un 21 conseguido con más de dos cartas.
La forma más directa, y sencilla, de intentar estudiar el juego es usando la Teoría de la Probabilidad. Dado un suceso o evento aleatorio mide el grado de certidumbre de que dicho suceso pueda ocurrir. Sea \(\Omega\) el espacio muestral, se define como una función de conjuntos de valor real \(P: \Omega \longrightarrow \mathbb{R}\ ([0,1])\) que satisface para un evento \(A\):
\(P(A)\geq 0\)
\(P(\Omega) = 1\)
Sea \(A_{1}, A_{2}, \ldots\) una secuencia contable de conjuntos disjuntos: \(P\Big( \bigcup_{i=1}^{\infty} A_i \Big)= \sum_{i=1}^{\infty} P(A_i)\)
Si los experimentos dan lugar a sucesos equiprobables, según la regla de Laplace: \[P(A) = \frac{\text{Nº de casos favorables}}{\text{Nº de resultados posibles}}\]
Independencia: \(P(A\cap B) = P(A)P(B)\)
Probabilidad condicional: \(P[A|B] = \frac{P[A\cap B]}{P[B]}\)
En el Blackjack usamos la baraja inglesa:
52 cartas en total.
4 palos: ♠ picas, ♥ corazones , ♦ diamantes, ♣ tréboles.
13 cartas para cada palo: \(A,2,3,4,5,6,7,8,9,10,J,Q,K\).
Cada carta es única.
Visto esto podemos ir estudiando las probabilidades de que nos toquen ciertas cartas en los sucesivos repartos. Por ejemplo, ¿probabilidad de obtener \(K\)?
\[P[K] = \frac{4}{52} = \frac{4}{4.13} = \frac{1}{13}\]
¿Probabilidad de obtener \(K\) si ya hemos sacado un \(K\) del mazo de cartas?
\[P[K|K] = \frac{4-1}{52-1} = \frac{3}{51} = \frac{1}{17}\]
Así la probabilidad de obtener pareja de reyes seguidos sería
\[P[K \cap K] = P[K] P[K|K] = \frac{4.3}{52.53} = \frac{1}{221}\]
y de esta forma podemos seguir calculando todas las combinaciones posibles, lo que conduce a la conocida como estrategia básica, que no es más que basar nuestra decisión en función de la frecuencia con la que ganaríamos dada la probabilidad de que se den esas cartas. Solo porque esta técnica se denomine “básica” no implica que deje de ser efectiva. Un jugador puede ganar una ventaja considerable mediante su aplicación. La Correlación de Apuestas (efectividad de apostar sobre la base de una cuenta de Altas-Bajas) es del 97%.
La parte que la película explica, desarrolla y dramatiza, es el estudio de lo que se conoce como el conteo de cartas. La idea detrás de un Sistema de Conteo de Cartas Altas-Bajas consiste en otorgarle un valor a cada carta, dividiendo todas las cartas en 3 grupos.
Si la totalidad de la baraja se suma de esta manera, la cuenta final tendrá como resultado, 0. Este método de Conteo de Cartas en el Blackjack le permite al jugador conocer cuáles cartas quedan (a grandes rasgos) en la baraja: cartas Altas o cartas Bajas. Cuando se encuentre a mitad de una baraja, si el valor de la cuenta mental es alto, significa que quedan más 10, figuras y ases en relación a la cantidad de cartas bajas. Esto representa una ventaja para el jugador. Si el valor es bajo, quedan más cartas bajas en la baraja, por lo general dándole ventaja al crupier.
Otras películas
- La gran apuesta \(\rightarrow\) ruina del jugador.
- El hombre que conocía el infinito \(\rightarrow\) particiones.
- Enigma \(\rightarrow\) Teoría de Códigos y Criptogrtafía.
- Los Simpsons y Futurama4.