Gran parte del dinero que ganarás al póker no procederá de la brillantez de tu juego, sino de la ineptitud de tus oponentes. Lou Krieger
VNM-Póker
El juego que se plantea en este capítulo a modo de ejemplo es el Póker de Von Neumann–Morgenstern, al que nos referiremos como VNM-Póker. Fue introducido en el estudio Theory of Games and Economic Behavior.
Existe una variante más compleja que desarrolló el matemático Harold William Kuhn conocida como Póker de Kuhn, entre otras.
Reglas
El juego consta de cuatro parámetros: \(S\), \(r\), \(n\), y \(m\), con \(m<n\). Hay cartas de valor 1 a \(S\) en un mazo, y cada valor ocurre \(r\) veces, \(S\cdot r\) cartas en total. Hay dos jugadores, \(Ann\) y \(Beth\). Cada jugador recibe aleatoriamente una carta del mazo, la mira, pero no se la muestra a su oponente. El ante es \(m\), lo que significa que ambos jugadores ponen \(m\) monedas, se suponen de igual valor, en el bote al comienzo del juego. La apuesta de cada jugador puede aumentar a \(n\) si el jugador pone \(n-m\) dólares adicionales. El juego es de suma cero.
\(Ann\) mueve primero eligiendo entre pasar (\(check\)), jugar por \(m\), o subir (\(raise\)), jugar por \(n\).
Si \(Ann\) pasa, ambas cartas se revelan y el jugador con la carta más alta obtiene el bote de \(2m\). En el caso de un empatar, obtener la misma carta, el dinero se divide en partes iguales y cada uno tiene lo mismo que al principio.
Si \(Ann\) sube, aumenta su apuesta total a \(n\). Entonces \(Beth\) tiene dos opciones, retirarse (\(fold\)) o ir (\(call\)).
Si \(Beth\) se retira, \(Ann\) obtiene el dinero del bote de \(n + m\), es decir, gana \(m\). La carta de \(Beth\) no se revela.
Si \(Beth\) va, aumenta su apuesta a \(n\). Entonces se revelan ambas cartas y el jugador con la carta más alta obtiene el \(2n\) en el bote; es decir, gana \(n\). En caso de empate, el dinero se divide en partes iguales.
Previamente
En primer lugar, se puede dar la forma extensiva del juego. Para ello es de rigor observar el módulo del juego que describe los movimientos de \(Ann\) y \(Beth\). Combinamos módulos para dotar al juego de su forma extensiva completa.
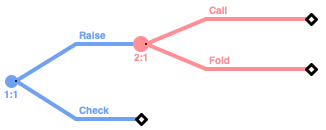
Se empieza con el reparto aleatorio de la carta, un nodo de riesgo. Supuesto \(r>1\), los jugadores pueden obtener cualquier carta de \(1,2,...,S\), existen \(S^2\) alternativas diferentes. Si \(r=1\), el número de alternativas sería de \(S\cdot(S-1)\).
Las alternativas para el movimiento aleatorio inicial no son igualmente probables. Por ejemplo, la probabilidad de obtener un \(King\) es \(\frac{r}{rS} = \frac{1}{S}\). Una vez que se ha sacado el \(King\) del mazo, quedan \(r-1\) \(King\) entre un total de \(rS-1\) cartas. De esta forma, la probabilidad de obtener un \(King\) es de \(\frac{r-1}{rS-1}\). En conclusión:
- Los casos donde \(Ann\) y \(Beth\) tienen cartas de igual valor \(x\), presentan probabilidad
\[p_{xx} = \frac{1}{S} \cdot \frac{r-1}{rS-1} = \frac{r-1}{S(rS-1)}.\]
- Los casos donde \(Ann\) y \(Beth\) tienen cartas de distinto valor, \(x\) e \(y\), presentan probabilidad
\[p_{xy} = \frac{1}{S} \cdot \frac{r}{rS-1} = \frac{r}{S(rS-1)}.\]
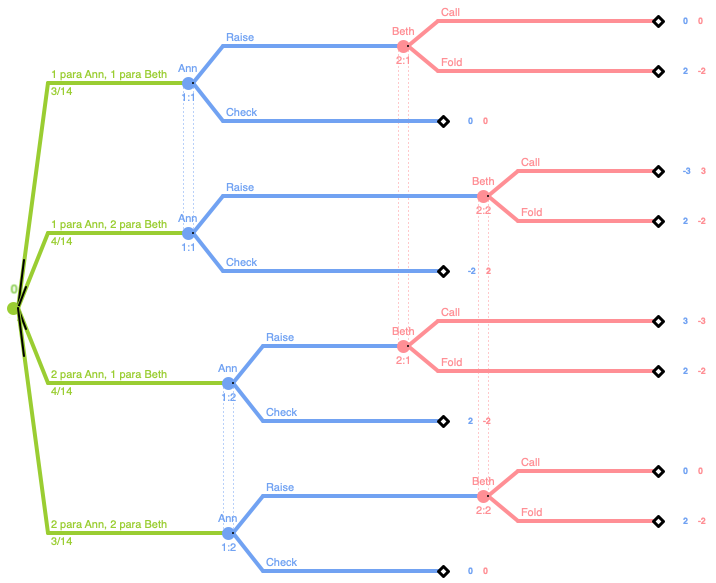
Estrategias
Si \(r>1\) hay \(S\cdot S\) diferentes combinaciones posibles de repartir un valor a \(Ann\) y otro a \(Beth\). \(Ann\) solo puede ver su carta y, por lo tanto, tiene \(S\) conjuntos de información. En cada uno puede elegir entre \(check\) o \(raise\). Es decir, Ann tiene \(2^S\) estrategias puras. Se codifican las estrategias por secuencias de \(R\) y \(C\); por ejemplo, \(RCCR\) para \(S=4\) significa que \(Ann\) \(raise\) con la carta más baja y la más alta y \(check\) con las dos cartas de valor medio. Por su parte, \(Beth\) también tendrá \(S\) conjuntos de información. En cada uno podrá elegir entre \(call\) o \(fold\). Por lo tanto, tiene \(2^S\) estrategias puras. Igualmente, las estrategias están codificadas por secuencias de \(C\) y \(F\).
Al final los pagos posibles son:
- \(Ann\) elige \(check\) \(\rightarrow\) \(m\), \(0\) ó \(-m\).
- \(Ann\) elige \(raise\) y \(Beth\) elige \(fold\) \(\rightarrow\) \(m\).
- \(Ann\) elige \(raise\) y \(Beth\) elige \(call\) \(\rightarrow\) \(n\), \(0\) ó \(-n\).
En nuestro caso, vamos a suponer que \(S=2\) y \(r\geq2\).
Bajo este supuesto se tiene que el conjunto de estrategias puras para \(Ann\) es {\(CC\) (prudente), \(CR\) (razonable), \(RC\) (inútil), \(RR\) (agresiva)} y para \(Beth\) se tiene {\(FF\) (prudente), \(FC\) (razonable), \(CF\) (contraintuitiva), \(CC\) (agresiva)}.
A continuación se presenta la forma normal de un juego VNM-Póker(2,r,m,n),

Las expresiones de esta tabla se obtienen de la siguiente forma. Para cada par de estrategias, sea \(u_{x,y}\) el pago que recibe \(Ann\) (al ser un juego de suma nula basta especificar solo una función de utilidad), siempre que ambos jugadores se ciñan a sus estrategias elegidas, dándose el caso de que \(Ann\) obtiene una carta de valor \(x\) y \(Beth\) una carta de valor \(y\). Entonces la utilidad esperada para \(Ann\) se calcula con la siguiente expresión
\[p_{xx} u_{1,1} + p_{xy} u_{1,2} + p_{xy} u_{2,1} + p_{xx} u_{2,2},\]
Con las probabilidades para cartas de mismo valor \(p_{xx}=\frac{r-1}{4r-2}\) y de distinto valor \(p_{xx}=\frac{r}{4r-2}\).
Por ejemplo, si \(Ann\) juega el \(RR\) y \(Beth\) juega el \(FC\) se tiene que \(u_{1,1} = m\), \(u_{1,2} = -n\), \(u_{2,1} = m\) y \(u_{2,2} = 0\) y por lo tanto el pago que recibe \(Ann\) es
\[\begin{aligned} & p_{xx} \cdot m + p_{xy} \cdot (-n) + p_{xy} \cdot m + p_{xx} \cdot 0 = \\ = & \frac{r-1}{4r-2}\cdot m + \frac{r}{4r-2}\cdot (-n) + \frac{r}{4r-2}\cdot m + \frac{r-1}{4r-2}\cdot 0 = \\ = & \frac{(r-1)m-rn+rm}{4r-2} = \\ = & \frac{(2r-1)m-rn}{4r-2}. \end{aligned}\]
Algunas estrategias puras son débilmente dominadas. Cuando \(Ann\) tiene una carta de mayor valor, \(raise\) domina a \(check\). Cualquiera de las estrategias de Ann \(X...YC\) donde \(Ann\) estaría débilmente dominada por la estrategia \(X...YR\). Cuando \(Beth\) tiene una carta de mayor valor, \(call\) domina a \(fold\). Cualquiera de las estrategias de \(Beth\) \(X...YF\) estaría débilmente dominada por \(X ... YC\).
De hecho, en el caso de \(Beth\), las relaciones de dominancia van más allá:
De esta forma eliminando las estrategias débilmente dominadas en nuestro ejemplo obtenemos la siguiente forma normal reducida,
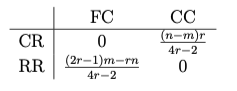
Por otra parte, existe un concepto en el póker denominado tirarse un farol, donde un jugador sube (\(raise\)) aunque tiene una carta (o mano) de poco valor. Debido a que un jugador puede tirarse un farol en un determinado momento del juego, las relaciones de dominancia deben analizarse con cuidado. No obstante, y supuesta la hipótesis de racionalidad de los jugadores, las relaciones de dominancia antes expuestas deben mantenerse.
Análisis del juego:
Equilibrio puro.
La entrada \(\frac{(n-m)r}{4r-2}\) es siempre positiva. Si \(\frac{(2r-1)m - rn}{4r-2}\) no es positivo, entonces la estrategia de \(Ann\) \(CR\) domina débilmente a \(RR\), y la estrategia de \(Beth\) \(FC\) domina débilmente a \(CC\). Por la tanto, hay un equilibrio de Nash puro \((CR,FC)\) con una utilidad esperada para \(Ann\) de 0.
El valor \(\frac{(2r-1)m - rn}{4r-2}\) es positivo cuando,
\[\frac{(2r-1)m - rn}{4r-2} \geq 0 \iff rn \geq (2r-1)m \iff \frac{n}{m} \geq \frac{2r-1}{r} \iff \frac{n}{m} \geq 2 - \frac{1}{r}.\]
Equilibrio mixto.
- ¿Cómo jugarías contra un jugador que no necesariamente juega de manera óptima, sino que mezcla las dos estrategias puras no dominadas arbitrariamente?
Si suponemos que somos \(Ann\) y asumimos que \(Beth\) juega una estrategia mixta: elige \(FC\) con probabilidad q y \(CC\) con probabilidad \(1-q\), i.e. \(Beth\) siempre elige \(call\) cuando tiene una carta de valor 2 y \(fold\) con probabilidad \(q\) cuando tiene una carta de valor 1.
¿Cuándo respondería \(Ann\) a la estrategia mixta con \(CR\) y cuándo con \(RR\)? Para esto estudiemos la mejor respuesta posible. El pago que recibe \(Ann\) al jugar \(CR\) es \(\frac{(1-q)(n-m)r}{4r-2}\) que es mayor o igual que el pago al jugar \(RR\), que es \(\frac{q((2r-1)m-rn)}{4r-2}\), si1
\[\begin{aligned} \frac{(1-q)(n-m)r}{4r-2} & \geq \frac{q((2r-1)m-rn)}{4r-2}\\(1-q)(n-m)r &\geq q((2r-1)m-rn) \\ (n-m)r - q(n-m)r & \geq q((2r-1)m-rn) \\ (n-m)r & \geq q[((2r-1)m - rn) + (n-m)r] \\ (n-m)r & \geq q[(r-1)m]. \end{aligned}\]
Como \(r\geq2\) se tiene que \((r-1)m > 0\) y por lo tanto,
\[q^* = \frac{(n-m)r}{(r-1)m} \geq q.\]
Ergo \(Ann\) debe jugar la estrategia razonable \(CR\), que no supone tirarse un farol, cuando \(Beth\) juega \(FC\) con probabilidad menor que \(q^*\), i.e. si \(Beth\) juega demasiado agresivo. En otro caso, \(Ann\) debería jugar la estrategia agresiva \(RR\). De la misma forma se puede analizar las mejores respuestas para \(Beth\).
Como conclusión, el análisis muestra que \(Ann\) debería jugar opuestamente al comportamiento que observe en \(Beth\). \(Beth\), por otro lado, debe imitar la jugada que observa en \(Ann\), ya sea agresiva o cautelosa. Esto advierte que la lectura del oponente es una parte fundamental del póker.
Si \(\frac{n}{m}\geq 2- \frac{1}{r}\), al no haber equilibrio de Nash puro, debe haber un equilibrio de Nash mixto.
Supóngase que \(Ann\) elige con probabilidad \(p\) y \(RR\) con probabilidad \(1-p\) y \(Beth\) juega \(FC\) con probabilidad \(q\) y \(CC\) con probabilidad \(1-q\). Dado que, como equilibrio de Nash, cada estrategia mixta es la mejor respuesta a la otra, y por lo tanto cada una de las estrategias puras \(CR\) y \(CC\), respectivamente \(FC\) y \(CC\), es una mejor respuesta a ellas, concluimos que
\[p = \frac{(2r-1)m-rn}{(r-1)m} \quad \text{y} \quad q = \frac{(n-m)r}{(r-1)m}.\]
Cálculo estrategias de comportamiento usando estrategias mixtas y viceversa.
Si consideramos en detalle el juego en forma extensiva, los dos conjuntos de información de \(Ann\) no tienen historial. Si se alcanzan o no depende de un movimiento aleatorio, pero no de los movimientos anteriores de \(Ann\), ya que ella no tiene ninguno.
Considérese una estrategia mixta de \(Ann\) de la forma \(p_1 [RR]+ p_2 [RC] + p_3 [CR] + p_4 [CC]\), donde \(p_1+p_2+p_3+p_4=1\). La estrategia de comportamiento correspondiente es elegir \(raise\) con probabilidad \(p_1 + p_2\) al obtener un 1 y con probabilidad \(p_3 + p_4\) al obtener un 2.
Supongamos ahora estrategia de comportamiento de \(raise\) en el \(40\%\) de los casos con un 1 y en el \(80\%\) de los casos con un 2. Si traducimos la estrategia de comportamiento a estrategias mixtas, obtenemos
\[\begin{aligned} p_1 & = p[RR] = 40\% \cdot 80\% = 32\%, \\p_2 & = p[RC] = 40\% \cdot 20\% = 8\%, \\ p_3 & = p[CR] = 60\% \cdot 80\% = 48\%, \\ p_4 & = p[CC] = 60\% \cdot 20\% = 12\%. \end{aligned}\]
El libro de Erich Prisner [pág 259-276] desarrolla en varios capítulos los juegos VNM-Póker(4,4,3,5), KUHN-Póker(3, 4, 2, 3) y End-of-Semester Poker Tournament explicados con detalle e incluyendo demostraciones.
En un juego con más de dos jugadores apostar por el equilibrio de Nash puede llevar a la derrota, resulta extremadamente difícil identificarlo y, además, en el póker hay mucha información escondida, por lo que no resulta práctico hacer esta aproximación. Sin embargo, el análisis de estos juegos sirve de base para la construcción de agentes automáticos de póker (bots) o desarrollo de distintos algoritmos para el estudio de las posibles estragegias (counterfactual regret minimization, EGT for extensive form games, …), e incluso para la formulación de diversos modelos económicos.

Obsérvese que bajo nuestro supuesto \(4r-2 >0\)↩︎