Análisis de Componentes Principales - datos USairpollution

Alberto Torrejón Valenzuela

2020/11/13

Categories: Estadística Tags: Minería Estadística ACP Ejemplo R

Ejemplo USairpollution

Los paquetes de R que vamos a emplear son:

# Lectura de datos
library(readr)
# Manipulación de datos
library(tidyverse)
library(magrittr)
# Gráficos
library(ggplot2)
library(ggforce)
library(ggthemes)

Los datos se pueden encontar en el paquete HSAUR3.

data("USairpollution", package="HSAUR3")

También se pueden cargar desde el directorio de trabajo.

aire.dat <- read_table2("Datos/datosaire.txt")
aire.dat %>% head()
# A tibble: 6 x 8
  Ciudad         SO2  Temp Empresas   Pob Viento Precip  Dias
  <chr>        <dbl> <dbl>    <dbl> <dbl>  <dbl>  <dbl> <dbl>
1 Phoenix         10  70.3      213   582    6     7.05    36
2 LittleRock      13  61         91   132    8.2  48.5    100
3 SanFrancisco    12  56.7      453   716    8.7  20.7     67
4 Denver          17  51.9      454   515    9    13.0     86
5 Hartford        56  49.1      412   158    9    43.4    127
6 Wilmington      36  54         80    80    9    40.2    114

Las variables recogidas en la base de datos son las siguientes:

  • Ciudad: nombre de la ciudad de EE.UU.
  • SO2: contenido de SO2 del aire en microgramos por metro cúbico.
  • Temp: temperatura media anual en grados Fahrenheit.
  • Empresas: número de empresas manufactureras que emplean 20 o más trabajadores.
  • Pob: tamaño de la población (censo de 1970) en miles.
  • Viento: velocidad media anual del viento en millas por hora.
  • Precip: precipitación media anual en pulgadas.
  • Dias: número medio de días con precipitación al año

Guardamos la variable Ciudad como nombres de la matriz y la quitamos para tener una matriz de datos numéricos. Es mejor usar el formato tibble en los datos que el dataframe por cuestiones de uso del paquete tidyverse, no obstante está modificación no es estrictamente necesaria para el buen desarrollo del ejercicio aunque la efectuaremos.

aire.dat <- aire.dat %>% as.tibble() %>% column_to_rownames("Ciudad")

Podemos realizar un estudio descriptivo de los datos para observar la singularidad de estos y advertir posibles anomalías. Además, complementaremos el análisis descriptivo con gráficos ilustrativos usando el paquete ggplot2, para lo que necesitaremos a menudo realizar una transformación, pivotado, de los datos para adecuarlos a la sintaxis del paquete e incluso emplear el paquete forcast para mejorar la visualización de los gráficos.

  • Análisis descriptivo.
aire.dat %>% summary()
      SO2              Temp          Empresas           Pob        
 Min.   :  8.00   Min.   :43.50   Min.   :  35.0   Min.   :  71.0  
 1st Qu.: 13.00   1st Qu.:50.60   1st Qu.: 181.0   1st Qu.: 299.0  
 Median : 26.00   Median :54.60   Median : 347.0   Median : 515.0  
 Mean   : 30.05   Mean   :55.76   Mean   : 463.1   Mean   : 608.6  
 3rd Qu.: 35.00   3rd Qu.:59.30   3rd Qu.: 462.0   3rd Qu.: 717.0  
 Max.   :110.00   Max.   :75.50   Max.   :3344.0   Max.   :3369.0  
     Viento           Precip           Dias      
 Min.   : 6.000   Min.   : 7.05   Min.   : 36.0  
 1st Qu.: 8.700   1st Qu.:30.96   1st Qu.:103.0  
 Median : 9.300   Median :38.74   Median :115.0  
 Mean   : 9.444   Mean   :36.77   Mean   :113.9  
 3rd Qu.:10.600   3rd Qu.:43.11   3rd Qu.:128.0  
 Max.   :12.700   Max.   :59.80   Max.   :166.0
  • Diagrama de cajas.
aire.dat %>%
  pivot_longer(everything(),names_to = "item",values_to = "valor") %>% 
  mutate(item = fct_reorder(item, valor, .fun='median')) %>%
  ggplot(aes(x=item, y=valor, fill=item)) +
    geom_boxplot() + theme_pander() + 
    theme(legend.position = "none") +
    xlab("") + ylab("")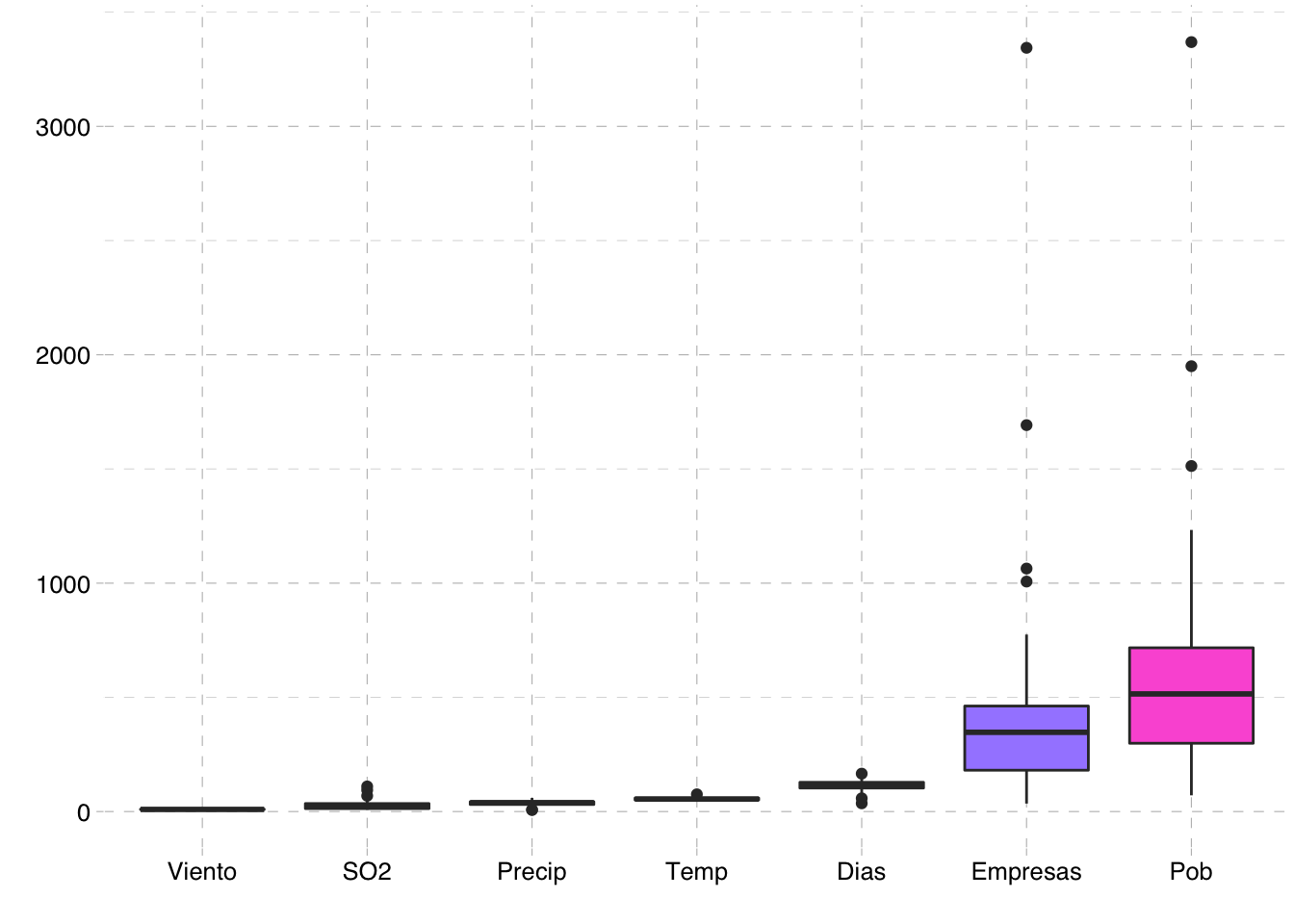

  • Gráfico de dispersión de parejas de variables. Se puede hacer llamando a la función pairs() implementada en R base pero para seguir con la sintaxis del paquete ggplot2 encontramos una opción en el paquete GGally que proporciona mucha más información con menor código.
library(GGally)
aire.dat %>% 
  ggpairs() + theme_pander() + 
  theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))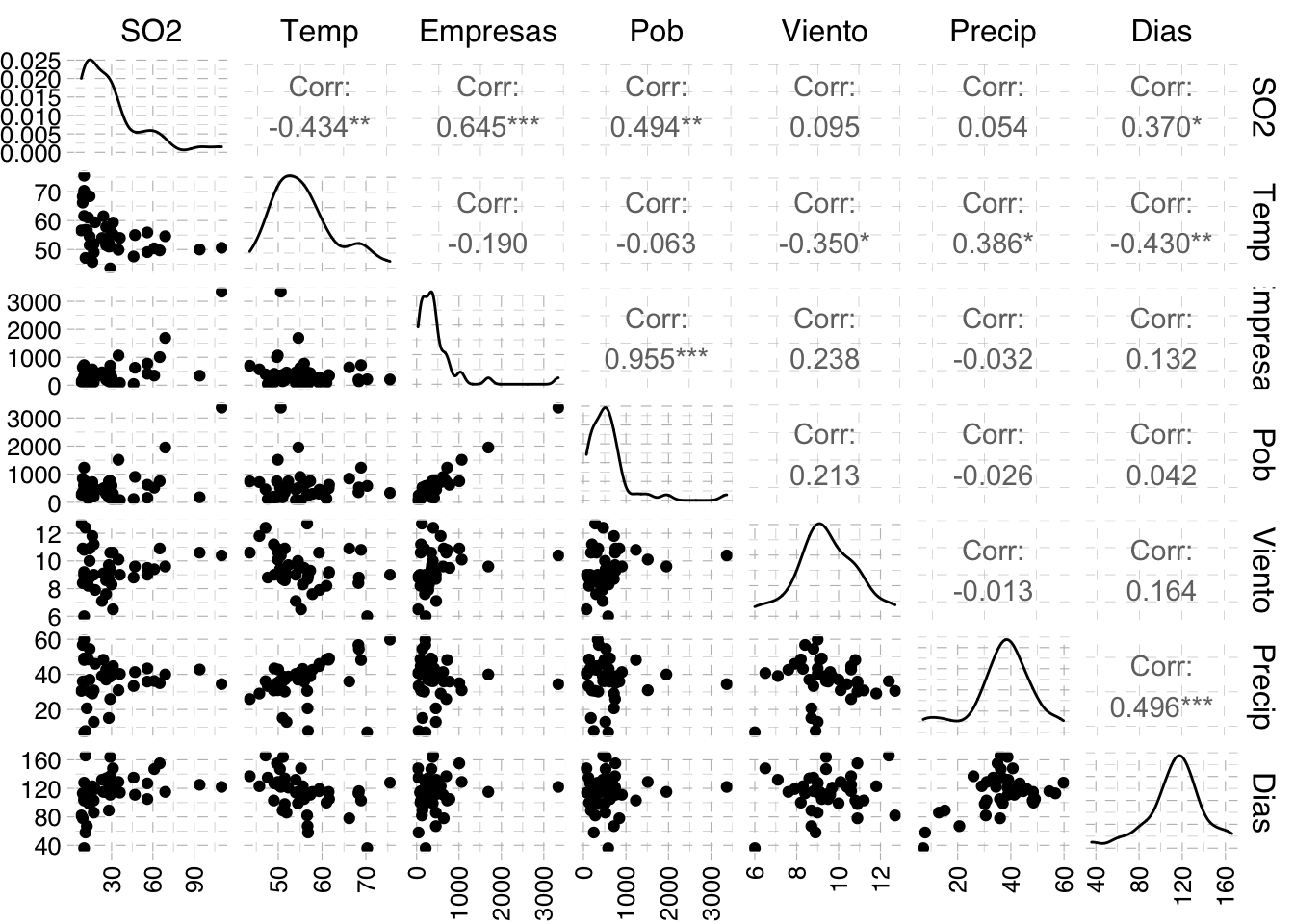

Los gráficos sugieren que pueden existir algunos valores atípicos en nuestra muestra. Por otra parte, en el diagrama de cajas podemos observar que las variables se miden en escalas bastante diferentes (unidades y rango de valores bastante diferentes), por lo que parece mejor trabajar con las variables estandarizadas. Además, encontramos que existen relaciones de colinealidad entre variables como por ejemplo entre Empresas y Pob. De hecho, como se comentaba en el desarrollo teórico anterior, para poder deducir conclusiones válidas del ACP es fundamental que exista correlación entre variables. Veamos si se cumple estudiando el determinante de la matriz de correlaciones.

  • Estudio de la correlación. Vamos a calcular la matriz de correlaciones, proyectar una visualización de esta reccurriendo al heatmap (se usará el paquete corrplot) y computar el determinante de la matriz.
R=cor(aire.dat)
round(R,2)
           SO2  Temp Empresas   Pob Viento Precip  Dias
SO2       1.00 -0.43     0.64  0.49   0.09   0.05  0.37
Temp     -0.43  1.00    -0.19 -0.06  -0.35   0.39 -0.43
Empresas  0.64 -0.19     1.00  0.96   0.24  -0.03  0.13
Pob       0.49 -0.06     0.96  1.00   0.21  -0.03  0.04
Viento    0.09 -0.35     0.24  0.21   1.00  -0.01  0.16
Precip    0.05  0.39    -0.03 -0.03  -0.01   1.00  0.50
Dias      0.37 -0.43     0.13  0.04   0.16   0.50  1.00
library(corrplot)
R %>%  corrplot(method = "square")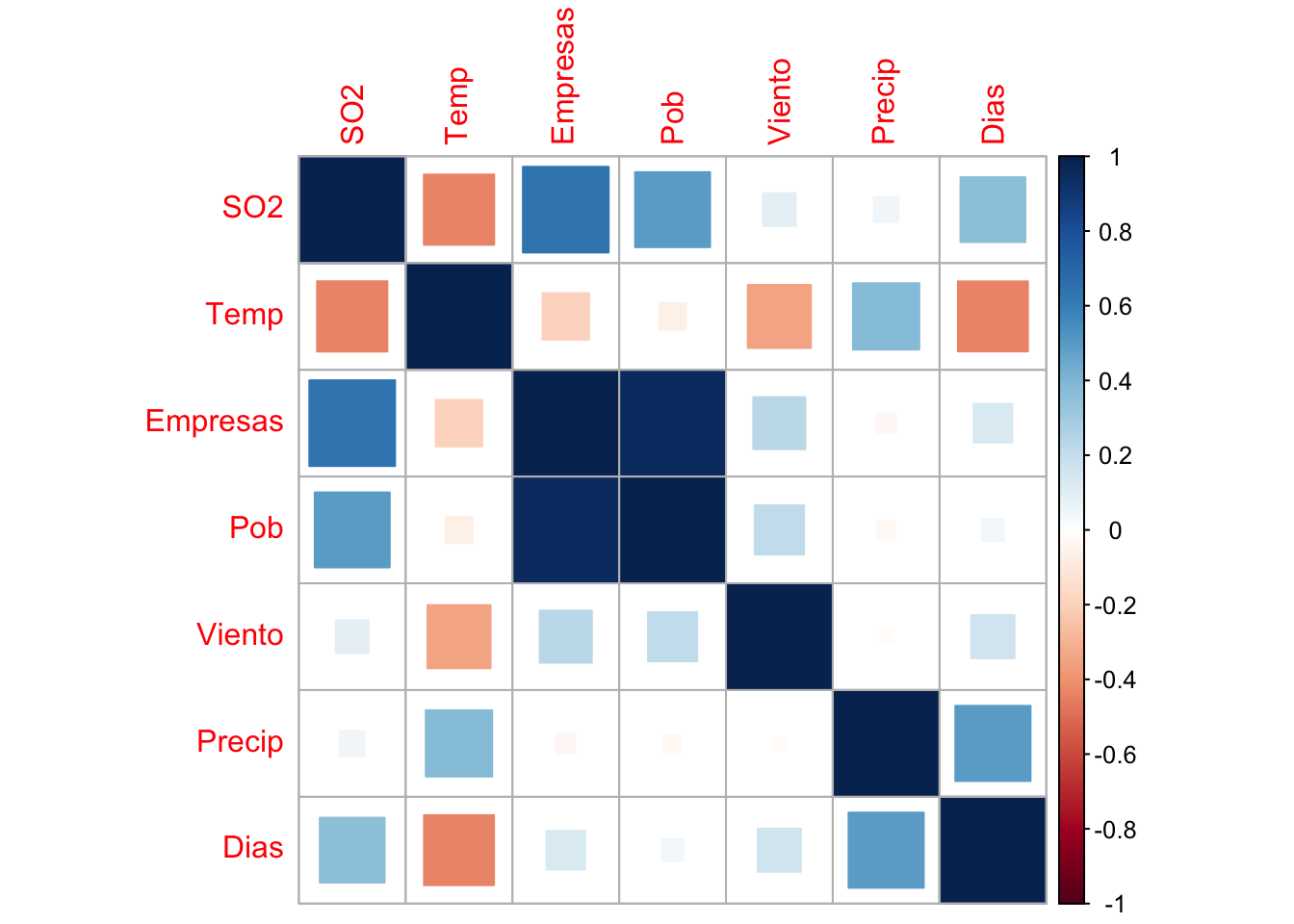

det(R)
[1] 0.004555454

El determinante de la matriz de correlaciones: un determinante muy bajo indicará altas intercorrelaciones entre las variables, pero no debe ser cero (matriz no singular), pues esto indicaría que algunas de las variables son linealmente dependientes y no se podrían realizar ciertos cálculos.

En nuestra matriz, dado que det(R) está cerca de cero, existe colinealidad y el ACP es apropiado para tratar con este conjunto de datos.

ACP con princomp

ORDEN:

  • princomp(formula, data = NULL, subset, na.action, ...)
  • princomp(x, cor = FALSE, scores = TRUE, covmat = NULL, subset = rep(TRUE, nrow(as.matrix(x))), ...)

ARGUMENTOS:

  • formula: fórmula sin variable respuesta, sólo con variables numéricas. Por ej.: ~ varX1 + varX2 + varX3.
  • data: un marco de datos opcional que contenga las variables de la fórmula.
  • subset: un vector opcional para seleccionar las filas (observaciones) de la matriz de datos.
  • x: matriz o marco de datos que proporciona los datos que proporciona los datos para el ACP.
  • cor: Valor lógico (T/F) indicando si se usa la matriz de correlación (T) o la matriz de covarianzas (F). Dado que debemos considerar las variables estandarizadas, o equivalentemente la matriz de correlación, cor = TRUE.
  • scores: Valor lógico (T/F) indicando si las puntuaciones de cada c.p. deben ser calculadas.

RESULTADOS: Crea un objeto princomp que recoge la siguiente información:

  • sdev: desviaciones estándar de las comp.principales.
  • loadings: matriz de cargas (es decir, matriz de autovectores).
  • center: las medias.
  • scaling: la escala aplicada a cada variable.
  • n.obs: número de observaciones.
  • scores: Si se ha solicitado, las puntuaciones de los datos en las c.p.
pca <- princomp(aire.dat, cor = TRUE)
pca
Call:
princomp(x = aire.dat, cor = TRUE)

Standard deviations:
   Comp.1    Comp.2    Comp.3    Comp.4    Comp.5    Comp.6    Comp.7 
1.6517021 1.2297702 1.1810897 0.9444529 0.5888792 0.3166822 0.1597339 

 7  variables and  41 observations.
pca %>% str()
List of 7
 $ sdev    : Named num [1:7] 1.652 1.23 1.181 0.944 0.589 ...
  ..- attr(*, "names")= chr [1:7] "Comp.1" "Comp.2" "Comp.3" "Comp.4" ...
 $ loadings: 'loadings' num [1:7, 1:7] 0.49 -0.315 0.541 0.488 0.25 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:7] "SO2" "Temp" "Empresas" "Pob" ...
  .. ..$ : chr [1:7] "Comp.1" "Comp.2" "Comp.3" "Comp.4" ...
 $ center  : Named num [1:7] 30.05 55.76 463.1 608.61 9.44 ...
  ..- attr(*, "names")= chr [1:7] "SO2" "Temp" "Empresas" "Pob" ...
 $ scale   : Named num [1:7] 23.18 7.14 556.56 572.01 1.41 ...
  ..- attr(*, "names")= chr [1:7] "SO2" "Temp" "Empresas" "Pob" ...
 $ n.obs   : int 41
 $ scores  : num [1:41, 1:7] -2.716 -1.718 -0.939 -0.55 0.46 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:41] "Phoenix" "LittleRock" "SanFrancisco" "Denver" ...
  .. ..$ : chr [1:7] "Comp.1" "Comp.2" "Comp.3" "Comp.4" ...
 $ call    : language princomp(x = aire.dat, cor = TRUE)
 - attr(*, "class")= chr "princomp"
pca %>% summary()
Importance of components:
                          Comp.1    Comp.2    Comp.3    Comp.4     Comp.5
Standard deviation     1.6517021 1.2297702 1.1810897 0.9444529 0.58887916
Proportion of Variance 0.3897314 0.2160478 0.1992819 0.1274273 0.04953981
Cumulative Proportion  0.3897314 0.6057792 0.8050611 0.9324884 0.98202821
                          Comp.6      Comp.7
Standard deviation     0.3166822 0.159733920
Proportion of Variance 0.0143268 0.003644989
Cumulative Proportion  0.9963550 1.000000000

La función de resumen en el objeto de resultado nos da la desviación estándar, la proporción de varianza explicada por cada componente principal y la proporción acumulada de varianza explicada. Recuérdese que la varianza del \(i\)-ésimo PC es el \(i\)-ésimo valor propio: \(\hat\sigma_{Y_i}^2 = \hat\lambda_i\).

Podemos construir nuestro propio resumen.

resumen_name <- paste0("CP",1:7)
resumen_eign <- pca$sdev^2
resumen_CP <- tibble(CP = resumen_name, Eigen = resumen_eign) %>% 
  mutate(Percentage = 100*Eigen/sum(Eigen),
         `Cumulative Percentage` = cumsum(Percentage))

resumen_CP %>%
  mutate_at(2:4, round, 2) %>% 
  kable()
CP Eigen Percentage Cumulative Percentage
CP1 2.73 38.97 38.97
CP2 1.51 21.60 60.58
CP3 1.39 19.93 80.51
CP4 0.89 12.74 93.25
CP5 0.35 4.95 98.20
CP6 0.10 1.43 99.64
CP7 0.03 0.36 100.00

Comprobamos que los valores propios de la matriz \(\mathbf{\hat R}\) concuerden con la varianza de los componentes principales.

eigen(R)$values
[1] 2.72811968 1.51233485 1.39497299 0.89199129 0.34677866 0.10028759 0.02551493

Selección del número de componentes

Podemos ver la variablidad explicada por cada componente construyendo un gráfico de autovalores o scree plot. Esto nos facilitará ver con qué componentes principales nos quedaremos siguiendo uno de los criterios anteriormente expuestos.

resumen_CP %>% 
  ggplot(aes(x = CP, y = Eigen)) + 
  geom_bar(stat="identity",width=0.01) + 
  geom_point() + theme_pander() +
  geom_hline(yintercept=1, linetype="dashed", color = "red")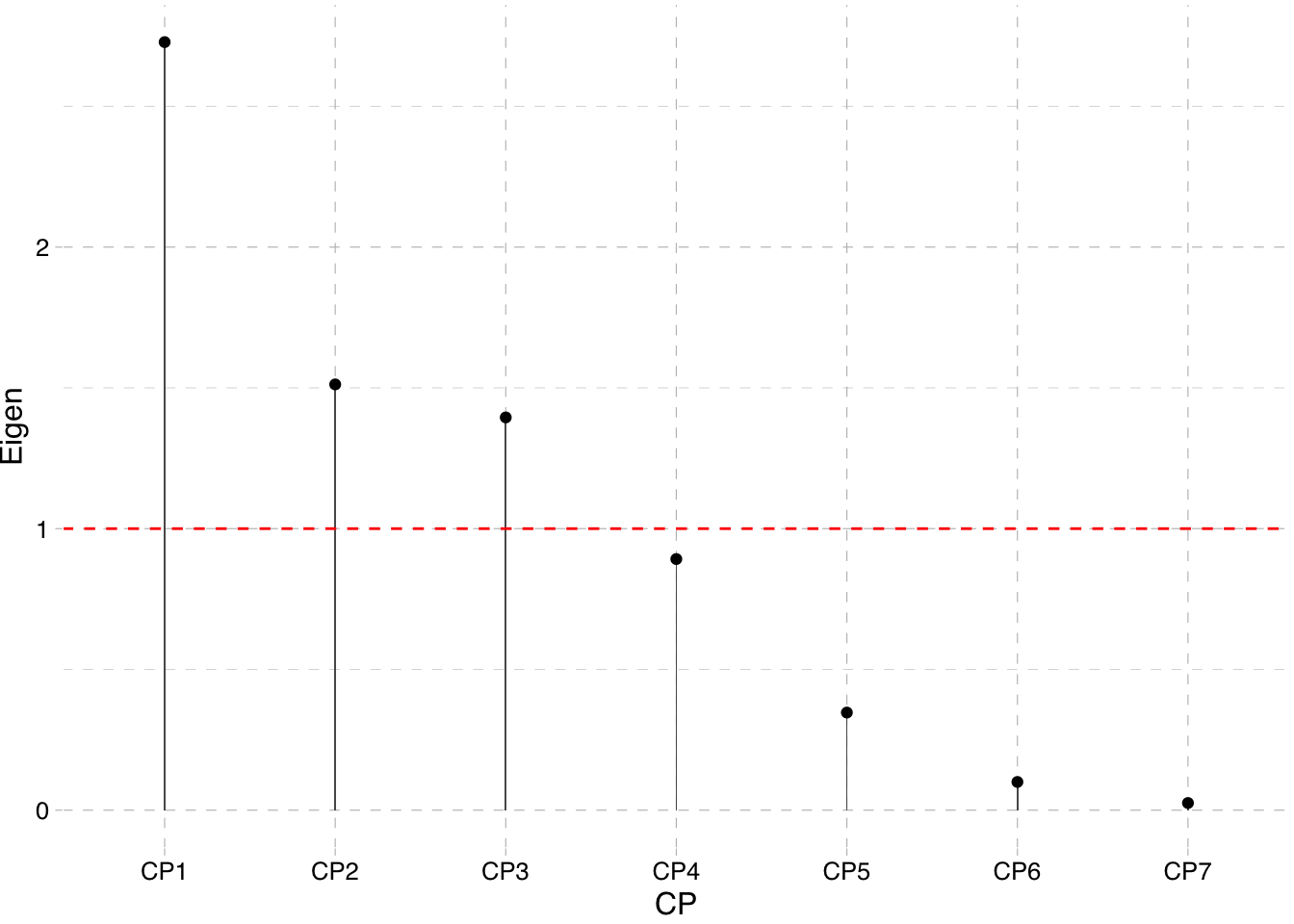

Para observar la variablidad explicada por cada CP existe una opción en el paquete de R base es llamando a plot directamente.

plot(pca, col = "lightblue")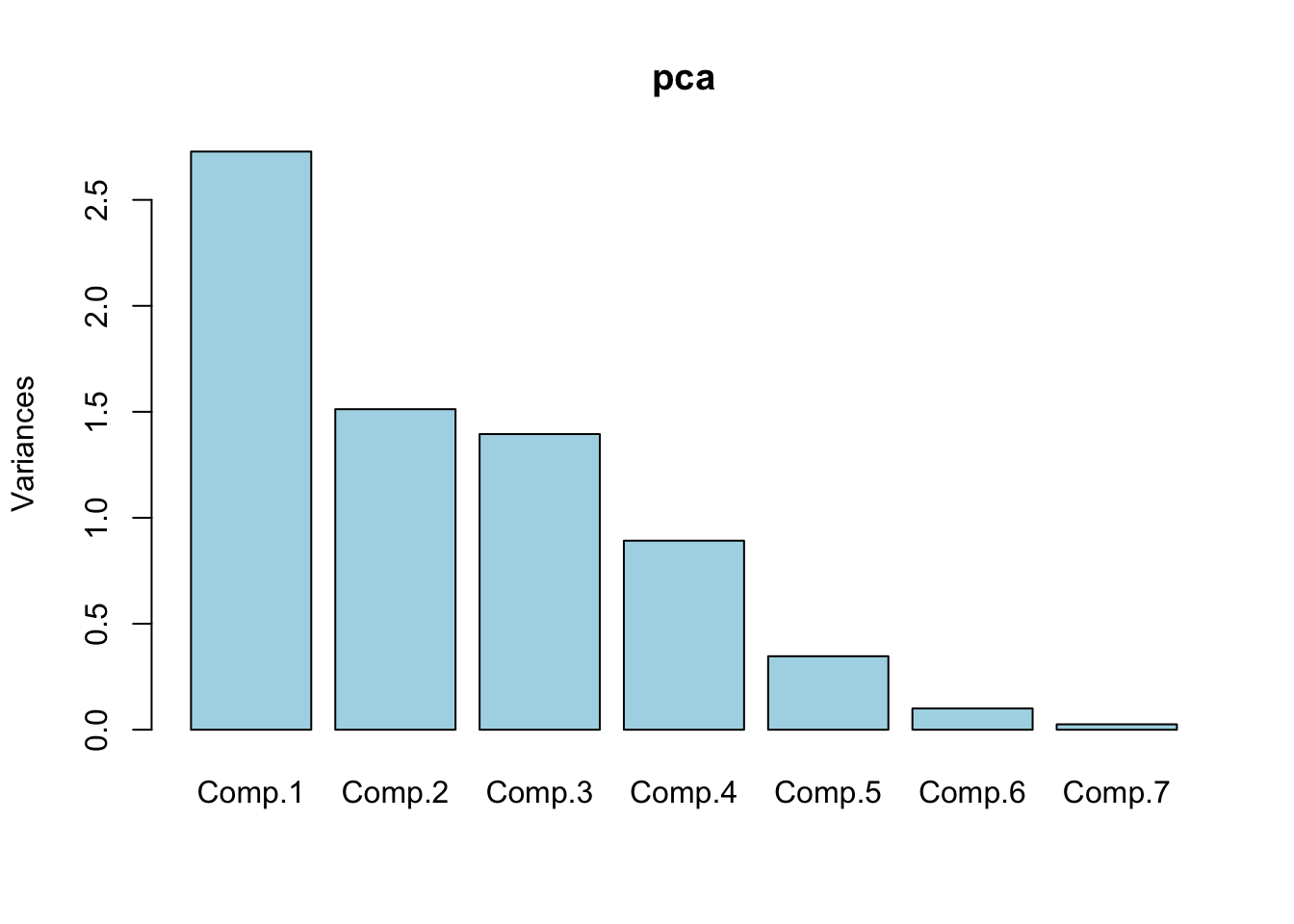

Tanto el resumen del ACP como ambos dibujos sugieren que en nuestro caso nos deberíamos de quedar con 3 componentes.

Estudio de las componentes

  • Cargas (loadings) de cada CP. Las conseguimos llamando a la orden loadings del paquete estadístico de R base. Las cargas pequeñas no se imprimen convencionalmente (siendo reemplazadas por espacios), para destacar los patrones de las cargas más grandes.
pca %>% loadings()

Loadings:
         Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
SO2       0.490                0.404  0.730  0.183  0.150
Temp     -0.315         0.677 -0.185  0.162  0.611       
Empresas  0.541 -0.226  0.267        -0.164        -0.745
Pob       0.488 -0.282  0.345 -0.113 -0.349         0.649
Viento    0.250        -0.311 -0.862  0.268  0.150       
Precip           0.626  0.492 -0.184  0.161 -0.554       
Dias      0.260  0.678 -0.110  0.110 -0.440  0.505       

               Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
SS loadings     1.000  1.000  1.000  1.000  1.000  1.000  1.000
Proportion Var  0.143  0.143  0.143  0.143  0.143  0.143  0.143
Cumulative Var  0.143  0.286  0.429  0.571  0.714  0.857  1.000

Recuérdese que las cargas son los coeficientes \(\underline{\hat e}_i\) que definen cada componente principal, \(Y_i = \underline{\hat e}_i'\underline{X}\). Así tenemos por ejemplo que la CP1 es

\[Y_1 = 0.41 SO2 - 0.315 Temp + 0.54Empresas + 0.488 Pob + 0.250 Viento + 0.26 Dias\]

y así con las demás. Las cargas coinciden con los autovectores de la matriz \(\mathbf{R}\). Comprobamos la relación (solo para \(Y_1\), \(Y_2\) e \(Y_3\)).

eigen(R)$vectors %>% 
  as.tibble() %>% 
  select(1:3) %>% 
  round(3) %>% 
  kable()
V1 V2 V3
0.490 -0.085 -0.014
-0.315 0.089 -0.677
0.541 0.226 -0.267
0.488 0.282 -0.345
0.250 -0.055 0.311
0.000 -0.626 -0.492
0.260 -0.678 0.110

Coinciden salvo signo.1

  • Correlación entre las variables originales \(X_i\) y las CP.

La relación de correlación viene dada por \[r_{X_i,Y_j} = \hat{e}_{ij}\sqrt{\hat\lambda_j}.\] Se pueden calcular de forma sencilla con la siguiente orden. Nos quedaremos con las dos primeras para posteriormente estudiar una representación gráfica de estas.

correlations <- loadings(pca)%*%diag(pca$sdev) 

corr_tibble <- correlations %>% 
  set_colnames(paste0("CP",1:7)) %>% 
  as.tibble() %>% mutate(nombre = rownames(correlations))
corr_tibble
# A tibble: 7 x 8
        CP1     CP2     CP3     CP4     CP5     CP6      CP7 nombre  
      <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>    <dbl> <chr>   
1  0.809     0.104   0.0169  0.382   0.430   0.0581  0.0239  SO2     
2 -0.521    -0.109   0.800  -0.175   0.0957  0.193  -0.00378 Temp    
3  0.894    -0.278   0.316  -0.0248 -0.0966 -0.0135 -0.119   Empresas
4  0.805    -0.347   0.407  -0.107  -0.206  -0.0278  0.104   Pob     
5  0.413     0.0682 -0.368  -0.814   0.158   0.0475  0.00252 Viento  
6  0.000309  0.770   0.581  -0.174   0.0946 -0.175  -0.00165 Precip  
7  0.430     0.834  -0.129   0.104  -0.259   0.160   0.00131 Dias    
corr_tibble %>% 
  select(c(1:2,8)) %>% 
  ggplot(aes(CP1,CP2,label=nombre)) + 
    xlim(-1,1) + ylim(-1,1) +
    geom_label() + 
    geom_hline(yintercept = -0.5, linetype="dashed", color = "red") +
    geom_hline(yintercept = 0.5, linetype="dashed", color = "red") +
    geom_vline(xintercept = -0.5, linetype="dashed", color = "red") +
    geom_vline(xintercept = 0.5, linetype="dashed", color = "red") + 
    theme_pander()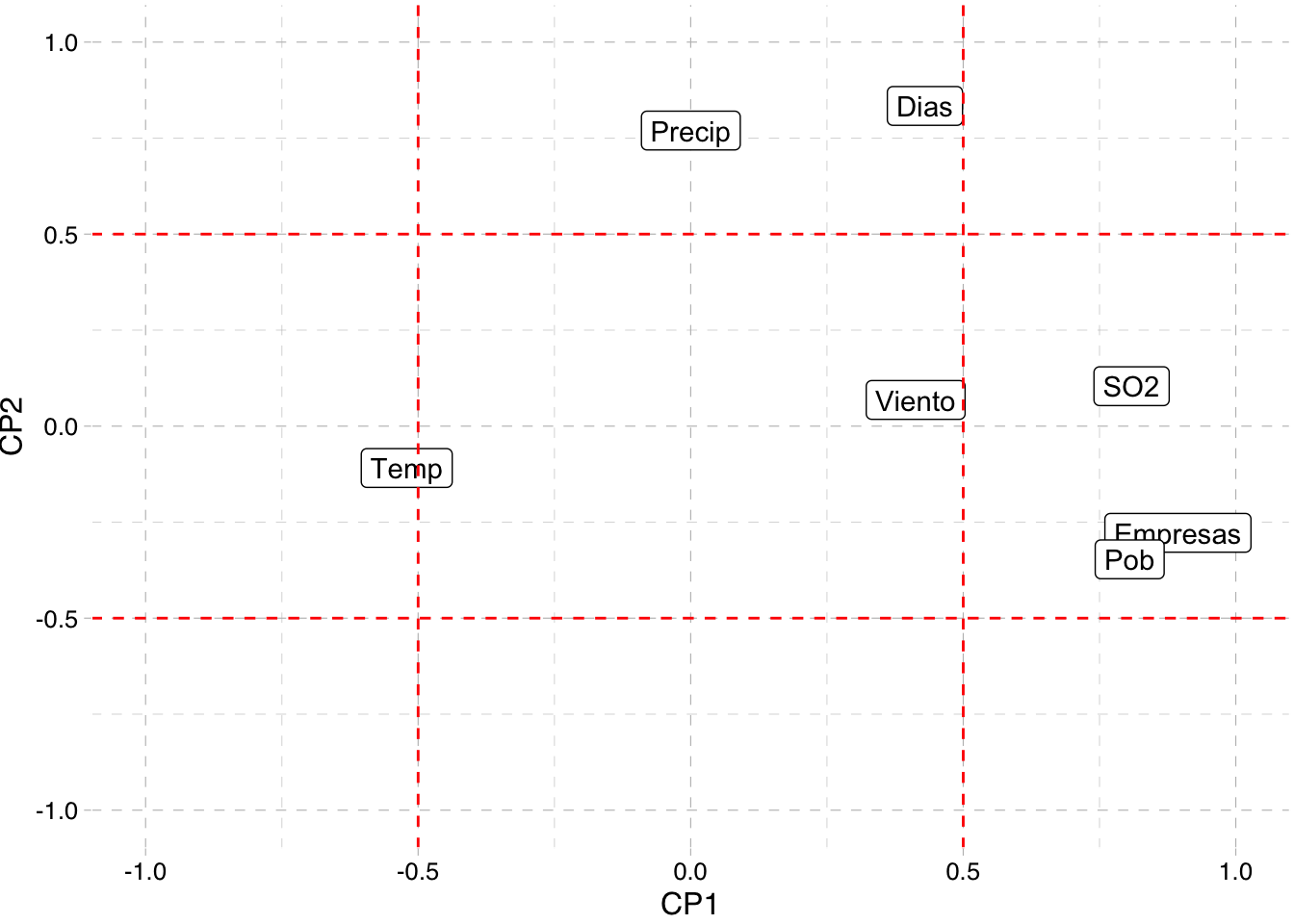

Este gráfico muestra cuáles de las variables originales están más fuertemente correlacionadas con las dos primeras CP. Podemos considerar más correladas aquellas que se encuentren fuera del cuadrado \([-.5,.5]\times[-.5,.5]\) (o también estudiar el valor absoluto). De nuevo, el gráfico puede verse rotado por la cuestión antes explicada del signo de los autovectores, pero la interpretación sigue siendo la misma.

Un gráfico al que se recurre para el estudio de la correlación entre variables y CP es el Círculo de Correlación. Se puede emplear el paquete FactoMineR como se indica en los apuntes. Otra opción es recurrir al paquete factoextra que hace un wrapper a funciones de ggplot2.

library(factoextra)
fviz_pca_var(pca, col.var = "salmon", 
             ggtheme = theme_pander())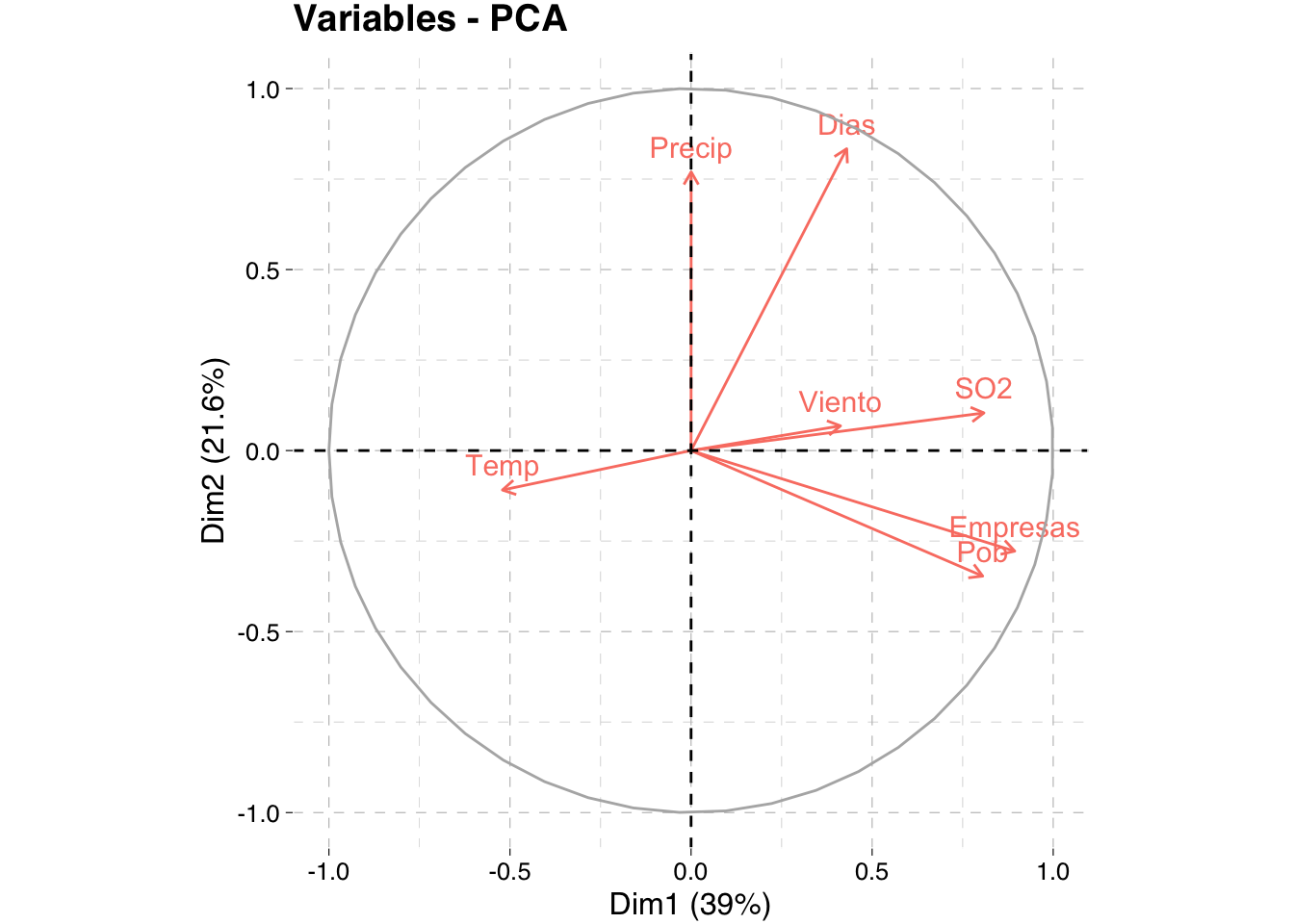

El círculo de correlación es un gráfico de \(r_{X_i,Y_1}\) versus \(r_{X_i,Y_2}\). Este gráfico muestra cuáles de las variables originales están más estrechamente correlacionadas con las PC, es decir, aquellas que están cerca de la periferia del círculo de radio 1. Con este gráfico también se puede observar la contribución de cada variable a las dos primeras componentes.

El argumento col.var puede ser una variable continua o una variable factorial. Los valores posibles incluyen: cos2, contrib, coord, x o y.

En este caso, los colores de los individuos/variables se controlan automáticamente por sus cualidades de representación (cos2), contribuciones (contrib), coordenadas (\(x^2 + y^2\), coord), valores x (x) o valores de y (y). Si se especifica solo un color es usado como único tono.

  • cos2: representa la calidad de representación de las variables y se calcula como las coordenadas cuadradas: \(var.cos2 = var.coord \times var.coord\). Para una variable dada, la suma del cos2 en todos los componentes principales es igual a uno. Si una variable está perfectamente representada por solo dos componentes principales (\(Dim.1\) y \(Dim.2\)), la suma del cos2 en estas dos CP es igual a uno. En este caso las variables se posicionarán en el círculo de correlaciones.Para algunas de las variables, se pueden requerir más de 2 componentes para representar perfectamente los datos. En este caso, las variables se colocan dentro del círculo de correlaciones.
fviz_cos2(pca, choice = "var", axes = 1:2,
             color = "salmon", fill = "cornflowerblue",
             ggtheme = theme_pander())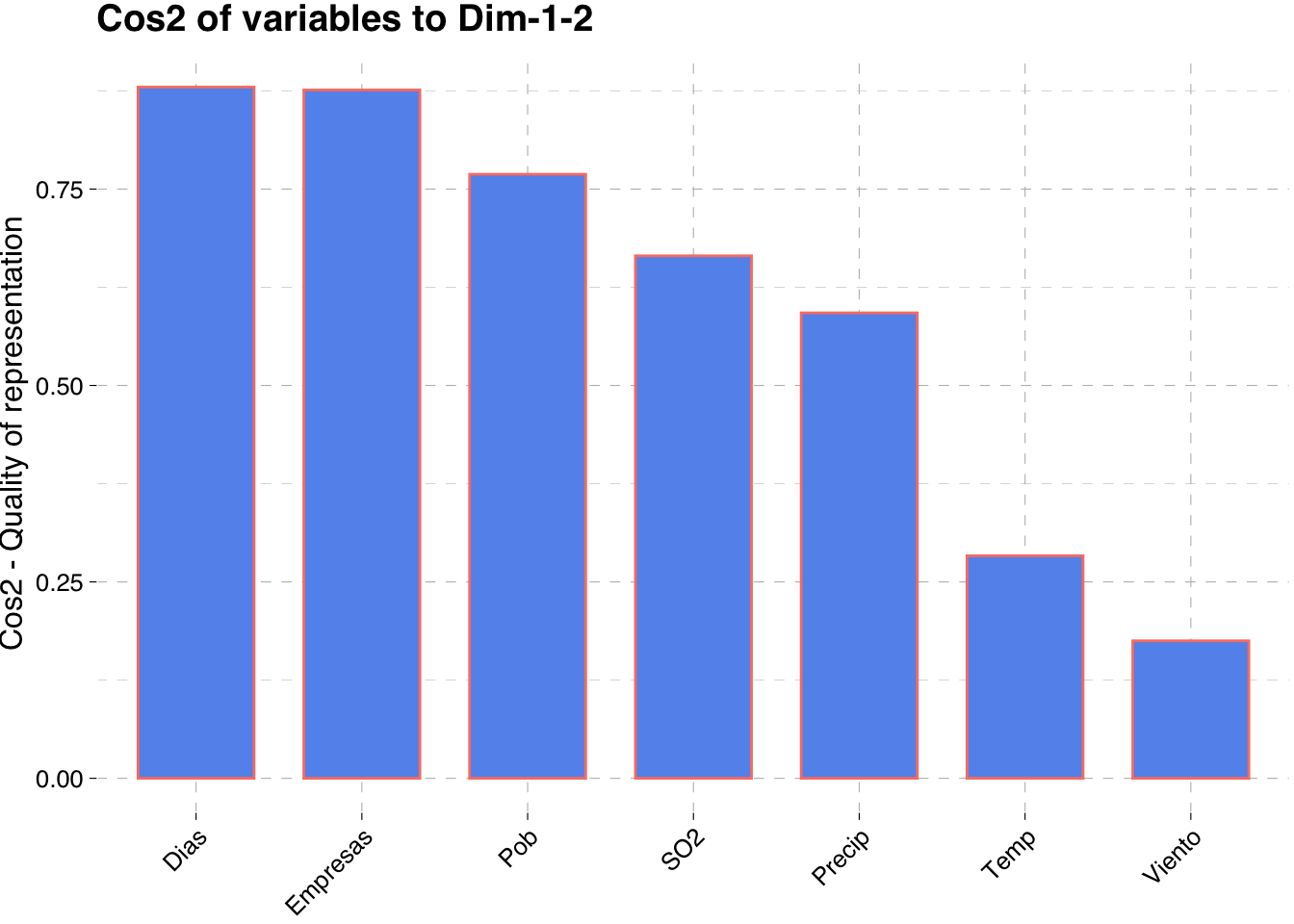

  • contrib: contiene las contribuciones (en porcentaje) de las variables a los componentes principales. La contribución de una variable (var) a un componente principal dado es (en porcentaje): \((var.cos2 \times 100) / (cos2 \ \text{total del componente})\). Las variables que están correlacionadas con CP1 (es decir, \(Dim.1\)) y CP2 (es decir, \(Dim.2\)) son las más importantes para explicar la variabilidad en el conjunto de datos. Las variables que no se correlacionan con ningún CP o que se correlacionan con las últimas dimensiones son variables de baja contribución y podrían eliminarse para simplificar el análisis general.

Es posible utilizar la función corrplot para resaltar las variables que más contribuyen a cada CP - dimensión:

var <- get_pca_var(pca)
var$contrib %>% round(3)
          Dim.1  Dim.2  Dim.3  Dim.4  Dim.5  Dim.6  Dim.7
SO2      23.980  0.715  0.021 16.339 53.348  3.362  2.236
Temp      9.946  0.786 45.851  3.431  2.639 37.291  0.056
Empresas 29.286  5.102  7.137  0.069  2.693  0.183 55.529
Pob      23.774  7.953 11.891  1.286 12.187  0.772 42.136
Viento    6.244  0.308  9.689 74.287  7.196  2.252  0.025
Precip    0.000 39.172 24.210  3.383  2.579 30.644  0.011
Dias      6.769 45.964  1.201  1.205 19.357 25.497  0.007
corrplot(var$contrib, is.corr=FALSE)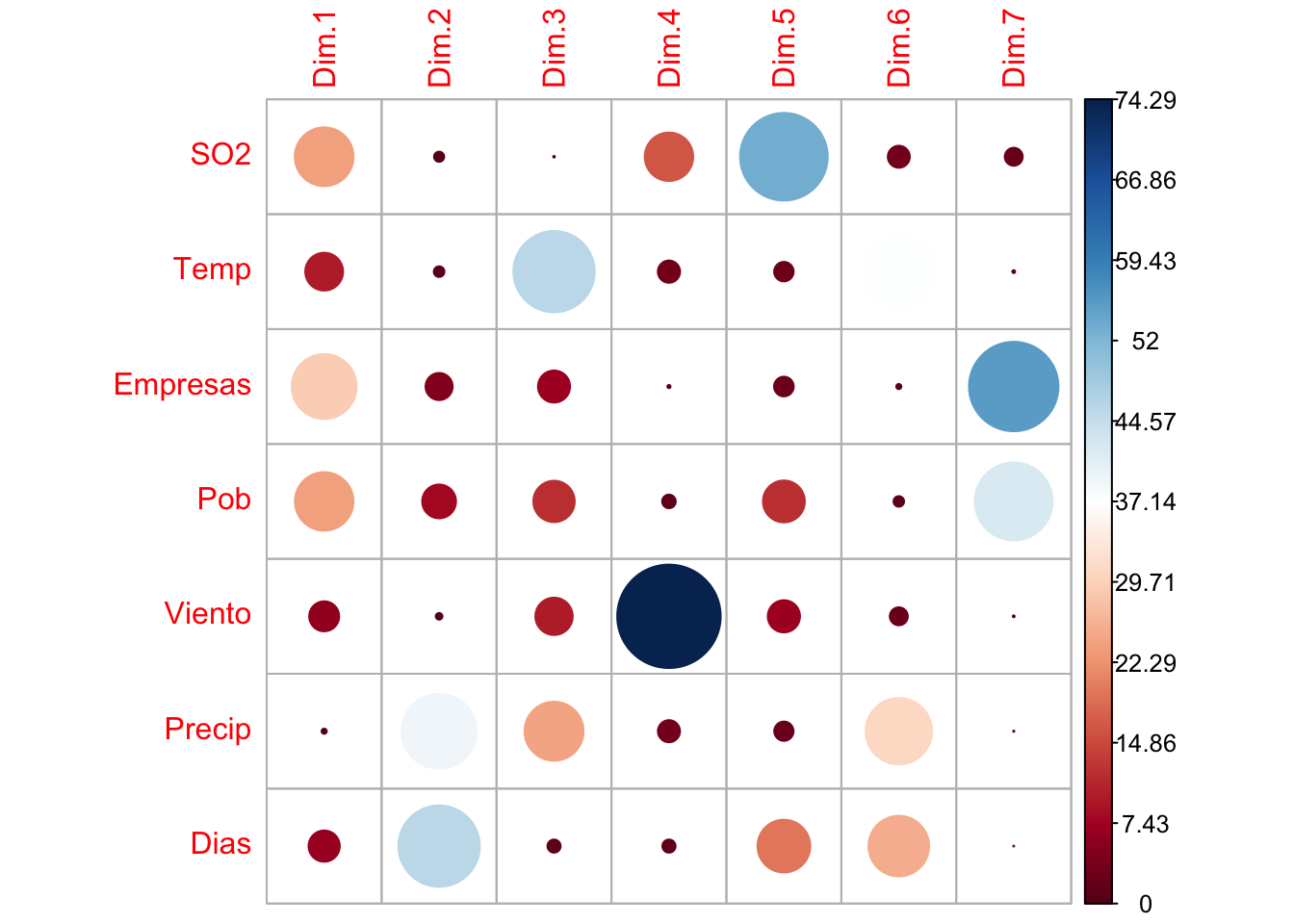

Cada cuadrado es un valor, círculos más oscuros y más grandes corresponden a valores más altos. La contribución total a CP1 y CP2 se obtiene con el siguiente código R:

fviz_contrib(pca, choice = "var", axes = 1:2, top = 10,
             color = "salmon", fill = "cornflowerblue",
             ggtheme = theme_pander())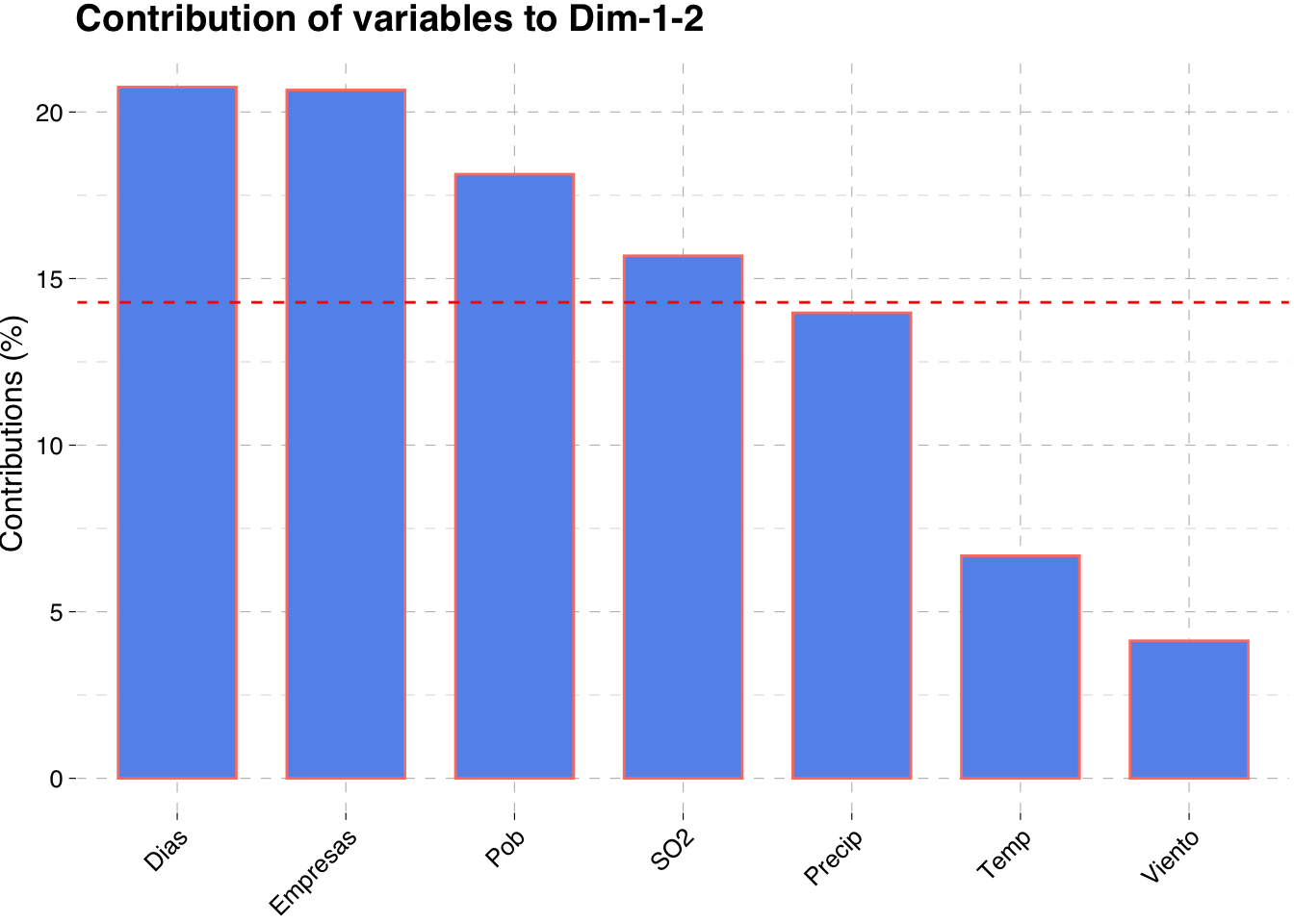

La línea roja discontinua en el gráfico indica la contribución promedio esperada. Si la contribución de las variables fuera uniforme, el valor esperado sería 1/longitud (variables) = \(1/10\) = \(10\%\). Para un componente dado, una variable con una contribución mayor que este límite podría considerarse importante para contribuir al componente. Lo que sugiere que las variables Temp y Viento no contribuyen mucho a las dos primeras componentes. No obstante en el apartado de selección de componentes se acordó que serían 3 las CP a elegir.

fviz_contrib(pca, choice = "var", axes = 1:3, top = 10,
             color = "salmon", fill = "cornflowerblue",
             ggtheme = theme_pander())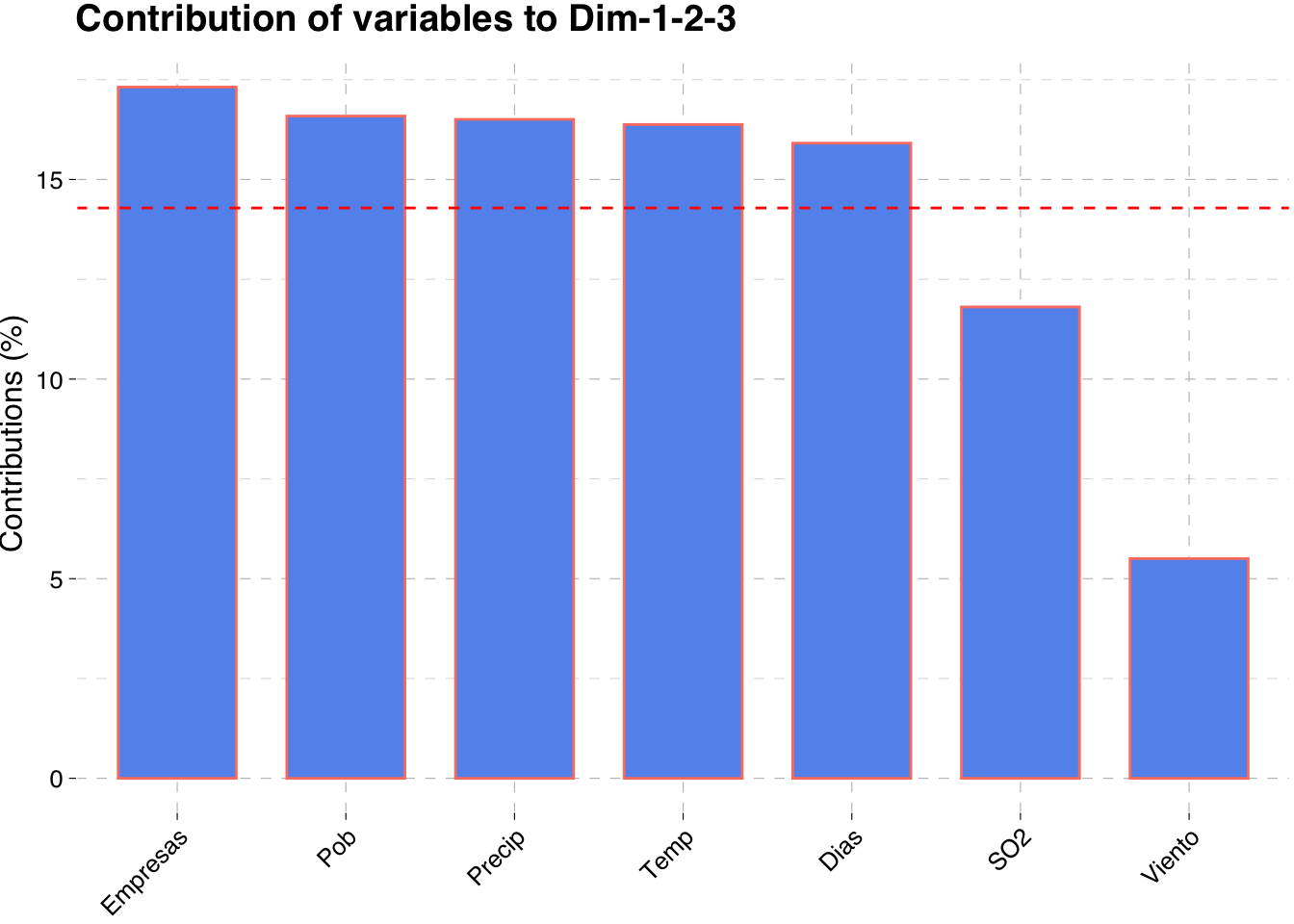

Lo que modifica la interpretación anterior.

Aquí se muestra el círculo de correlación indicando la contribución de las variables a las 2 primeras CP.

fviz_pca_var(pca, col.var = "coord",
   gradient.cols = c("orange", "red", "blue"),
   ggtheme = theme_pander())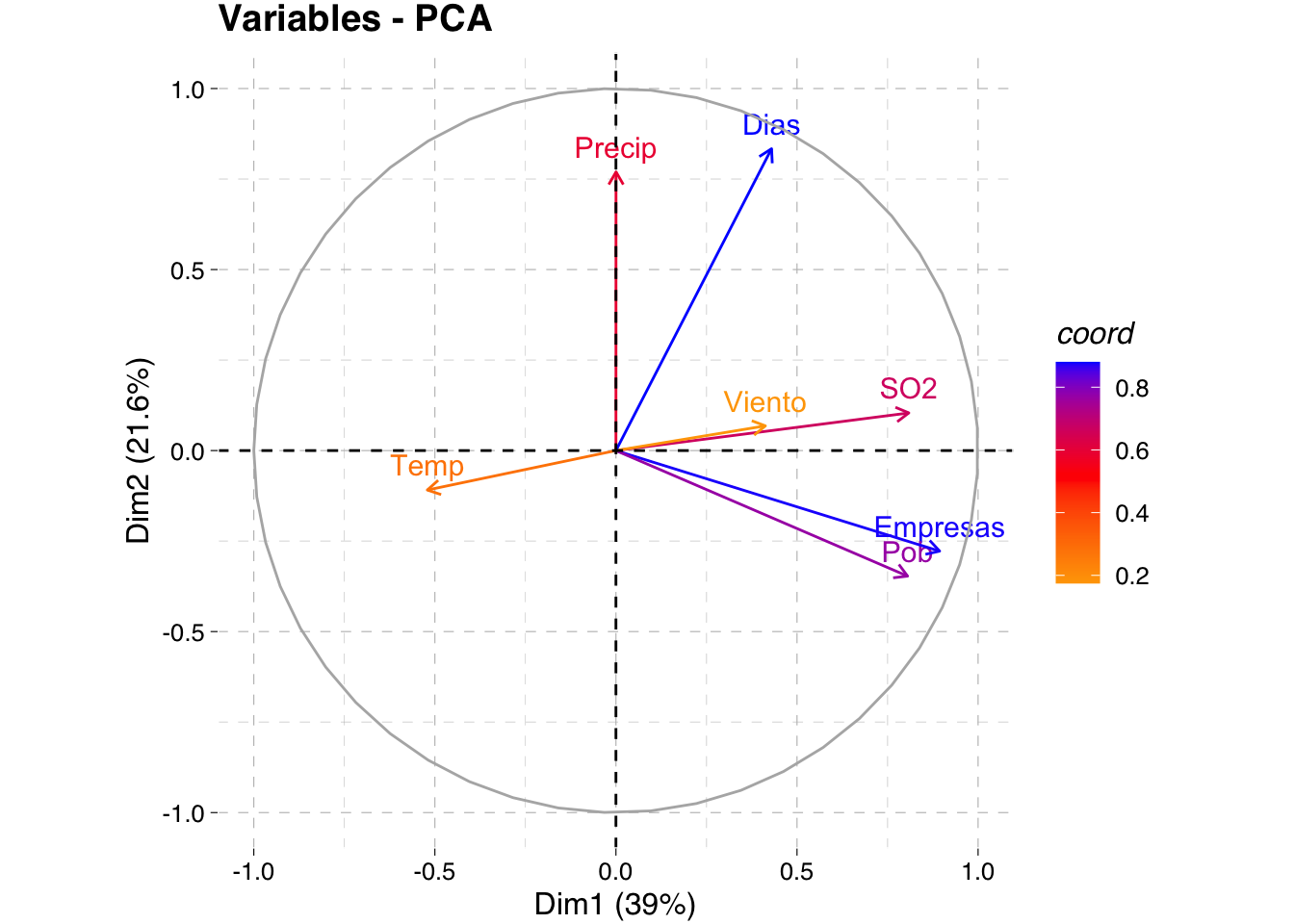

  • Gráfico de las puntuaciones

Las puntuaciones son los valores de las CP en las unidades de muestra.

pca$scores %>% head() %>% kable()
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
Phoenix -2.7159758 -3.8914391 1.0583546 1.5374428 0.0331333 0.6544276 0.0906066
LittleRock -1.7177454 0.4824200 0.8500434 0.1945366 0.1421327 -0.5449915 -0.1986651
SanFrancisco -0.9389649 -2.2372464 -0.1837479 0.1527907 -0.1855924 -0.2950736 0.0071357
Denver -0.5498615 -1.9719430 -1.2285958 0.4226922 -0.3836845 0.1301060 -0.1579881
Hartford 0.4603718 1.0973345 -0.5897038 0.9387046 0.7426900 -0.4004830 -0.2601886
Wilmington -0.6970761 0.6321489 -0.4213294 0.4888693 0.5449854 -0.2042173 -0.0507348

Podemos representarlas para la CP1 y la CP2. Se podría hacer recurriendo al paquete base de R con plot() o empleando el paquete ggplot, pero aprovechando que se ha introducido el paquete factoextra se usará la función fviz_pca_ind() que permite usar las herramientas de ggplot de forma más intuitiva.

fviz_pca_ind(pca, col.ind = "cornflowerblue", 
             gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
             repel = TRUE, ggtheme = theme_pander())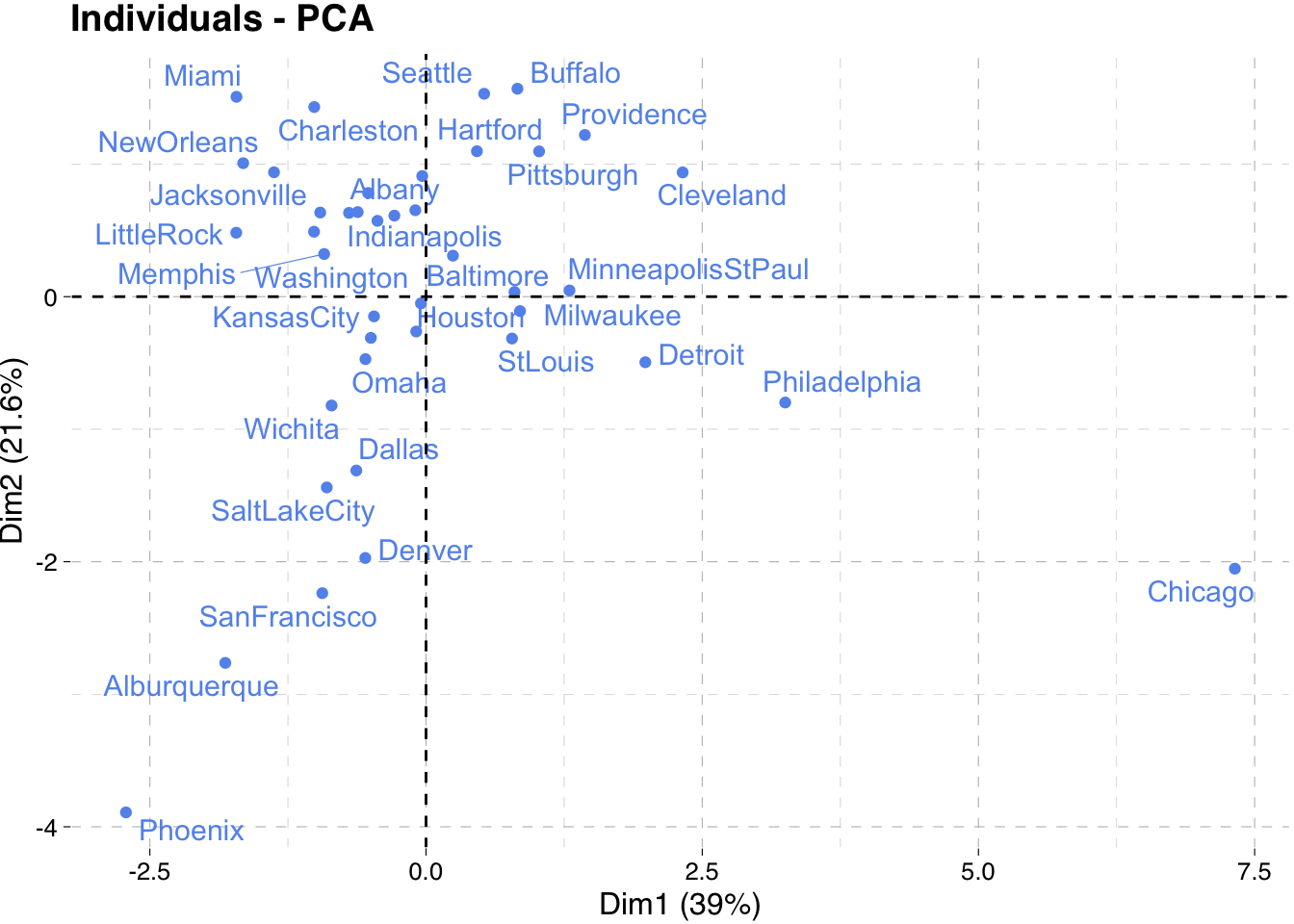

Este gráfico es útil para detectar valores atípicos en el caso multivariado. En este ejemplo, Chicago y Phoenix pueden ser valores atípicos. El gráfico puede verse rotado de nuevo al replicarlo como se explicó anteriormente.

  • Biplot

Todo lo anterior se puede agrupar fácilmente en un gráfico conjunto que se conoce como biplot. En el paquete factoextra se encuentra la orden fviz_pca_biplot que permite construir este gráfico de forma intuitiva y haciendo uso del motor de ggplot2.

fviz_pca_biplot(pca,
                col.var = "red", # Variables color
                col.ind = "cornflowerblue",  # Individuals color
                repel = TRUE, ggtheme = theme_pander())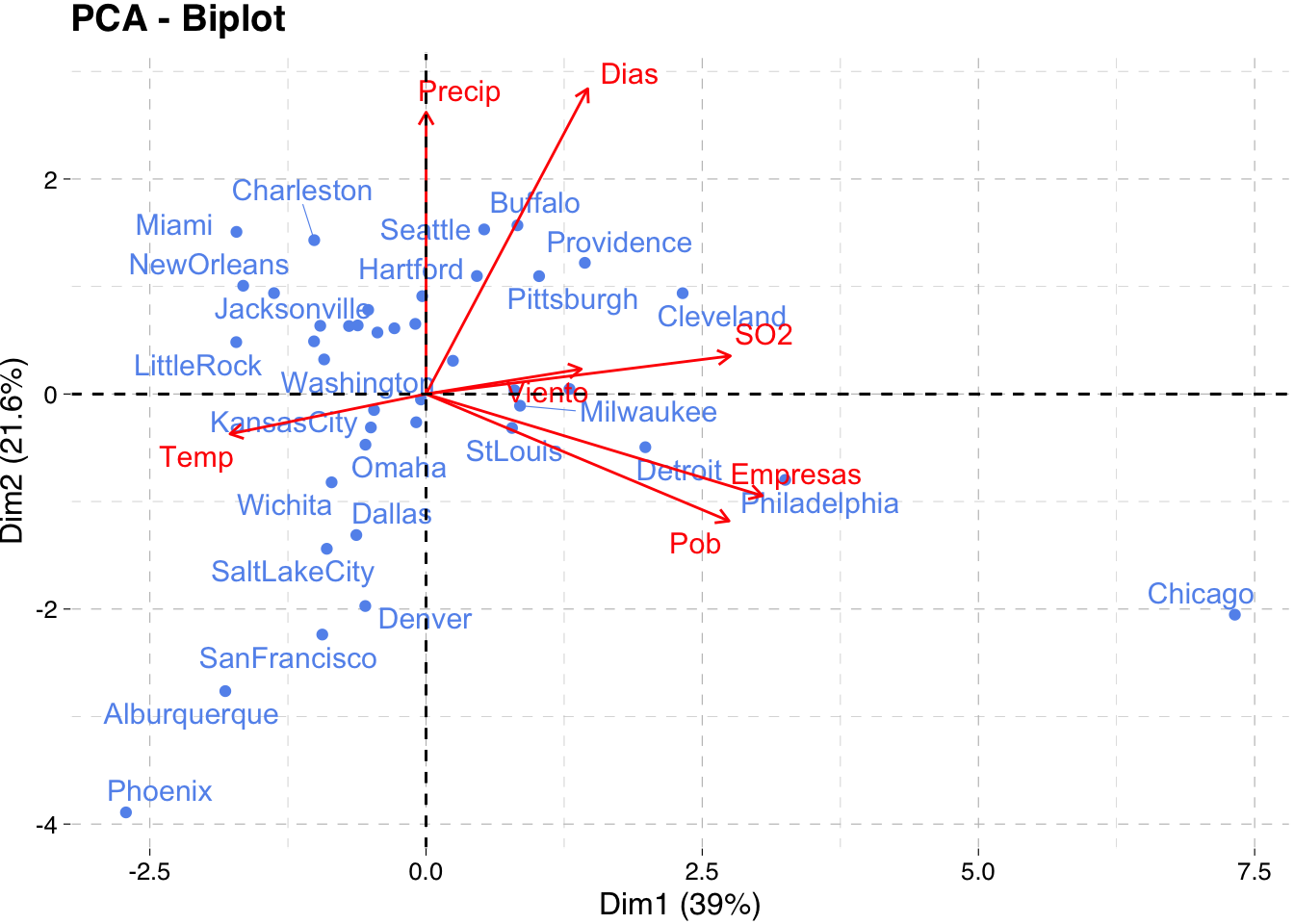

Tenga en cuenta que el biplot solo puede ser útil cuando hay un número bajo de variables e individuos en el conjunto de datos; de lo contrario, la trama final sería ilegible. Tenga en cuenta también que las coordenadas de los individuos y las variables no se construyen en el mismo espacio. Por lo tanto, en el biplot, debe centrarse principalmente en la dirección de las variables, pero no en sus posiciones absolutas en el gráfico.

En términos generales, un biplot se puede interpretar de la siguiente manera:

  • Un individuo que está en el mismo lado de una variable dada tiene un valor alto para esta variable.
  • Un individuo que está en el lado opuesto de una variable dada tiene un valor bajo para esta variable.

A continuación, comprobamos que la variabilidad de la PC disminuye

\[\hat\lambda_1 \geq \hat\lambda_2 \geq \cdots \geq \hat\lambda_7\]

pca$scores
                       Comp.1      Comp.2      Comp.3      Comp.4      Comp.5
Phoenix           -2.71597577 -3.89143908  1.05835456  1.53744284  0.03313329
LittleRock        -1.71774538  0.48242002  0.85004335  0.19453662  0.14213267
SanFrancisco      -0.93896495 -2.23724644 -0.18374788  0.15279070 -0.18559238
Denver            -0.54986148 -1.97194298 -1.22859584  0.42269224 -0.38368448
Hartford           0.46037184  1.09733455 -0.58970378  0.93870455  0.74269000
Wilmington        -0.69707612  0.63214894 -0.42132942  0.48886932  0.54498541
Washington        -0.04612550 -0.05089780  0.35423200 -0.04402514 -0.02934285
Jacksonville      -1.37601389  0.93839689  1.86596320 -0.45438597  0.01384513
Miami             -1.71572800  1.50799472  2.58526278 -0.82939956  0.05685634
Atlanta           -0.61858862  0.63808943  0.98836295 -0.19607655  0.11214859
                         Comp.6       Comp.7
Phoenix            0.6544276475  0.090606552
LittleRock        -0.5449915353 -0.198665115
SanFrancisco      -0.2950735876  0.007135691
Denver             0.1301060178 -0.157988070
Hartford          -0.4004830221 -0.260188627
Wilmington        -0.2042172800 -0.050734764
Washington        -0.0696776892  0.191097207
Jacksonville       0.1205695112  0.179974967
Miami              0.7195496265 -0.183303486
Atlanta           -0.0989937572 -0.071121250
 [ reached getOption("max.print") -- omitted 31 rows ]
pca$scores %>% 
  as.tibble() %>%
  pivot_longer(everything(),names_to = "item",values_to = "valor") %>% 
  ggplot(aes(x=item, y=valor, fill=item)) +
    geom_boxplot() + theme_pander() + 
    theme(legend.position = "none") +
    xlab("") + ylab("")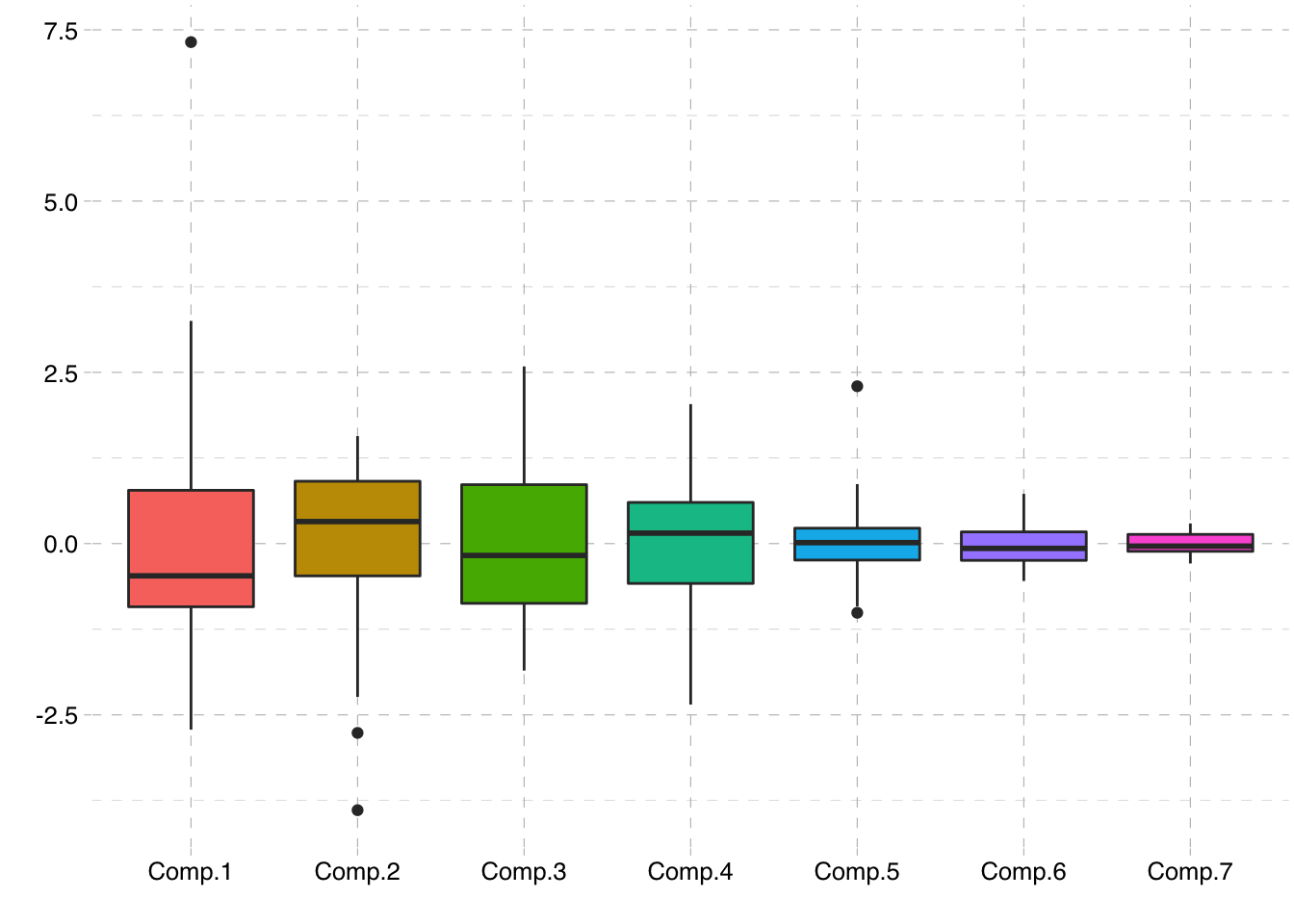

Podemos usar el comando boxplot para detectar los valores atípicos en nuestros datos.

boxPCA = boxplot(pca$scores)
outliers = boxPCA$out
outliers
[1]  7.320800 -3.891439 -2.763310 -1.009775  2.297055
component=boxPCA$group
component
[1] 1 2 2 5 5

Se puede comprobar que los valores atípicos detectados por CP1 y CP2 corresponden a Chicago, Phoenix y Alburquerque.

Ampliación - Usando tidymodels

library(tidymodels)

¿Porque tidymodels?

R es un software de licencia abierta que cuenta con una comunidad activa que es a la vez desarrolladora y explotadora de los paquetes disponibles para su uso. Desde hace un tiempo, un grupo de estos miembros, entre los que cabe destacar a Hadley Wickham o Julia Silge entre otros, llevan centrando sus esfuerzos en organizar y facilitar el uso de R como herramienta creando el tidyverso, mundo ordenado. A esta iniciativa se están uniendo otros muchos desarrolladores que dejan de actualizar sus paquetes para integrarlos en los que se están desarrollando, quedando estos desfasados y en algunos casos desactualizados para nuevas versiones de R.

Esta idea bajo la cual se construye el paquete tidymodels, donde se están recogiendo los principales modelos de aprendizaje e incorporándolos en un flujo de trabajo que facilite su programación y análisis.

Este apartado pretende mostrar los pasos para construir un análisis de componentes principales - PCA - con el paquete tidymodels sobre los datos de USairpollution descritos en el apartado anterior. No nos detendremos tanto en las conclusiones y las interpretaciones de los resultados debido a que se han expuesto en el apartado anterior, así como nos preocuparemos del código necesario.

Seguimos trabajando con los mismos datos.

aire.dat
             SO2 Temp Empresas Pob Viento Precip Dias
Phoenix       10 70.3      213 582    6.0   7.05   36
LittleRock    13 61.0       91 132    8.2  48.52  100
SanFrancisco  12 56.7      453 716    8.7  20.66   67
Denver        17 51.9      454 515    9.0  12.95   86
Hartford      56 49.1      412 158    9.0  43.37  127
Wilmington    36 54.0       80  80    9.0  40.25  114
Washington    29 57.3      434 757    9.3  38.89  111
Jacksonville  14 68.4      136 529    8.8  54.47  116
Miami         10 75.5      207 335    9.0  59.80  128
Atlanta       24 61.5      368 497    9.1  48.34  115
 [ reached 'max' / getOption("max.print") -- omitted 31 rows ]

En primer lugar, para usar tidymodels, debemos definir un pipeline, es decir, una serie de pasos de análisis que queremos realizar. Para ello empleamos el paquete R recipes.

pca_recipe <- recipe(~., data = aire.dat)

Como el ACP es un algoritmo de aprendizaje no supervisado no habrá que realizar la partición del conjunto de datos característico de los modelos de aprendizaje supervisado. No obstante, si que habrá que preprocesar los datos para adecuarlos al ACP escalando los datos. Y finalmente, especificamos que queremos hacer PCA usando step_pca().

pca_trans <- pca_recipe %>%
  step_center(all_numeric()) %>% # center the data
  step_scale(all_numeric()) %>% # center the data
  step_pca(all_numeric()) # pca on all numeric variables
pca_trans
Data Recipe

Inputs:

      role #variables
 predictor          7

Operations:

Centering for all_numeric()
Scaling for all_numeric()
No PCA components were extracted.

Ahora estamos listos para el análisis. Usaremos la receta que construimos hasta ahora como argumento para la función prep(), “preparar”.

pca_estimates <- prep(pca_trans)
pca_estimates
Data Recipe

Inputs:

      role #variables
 predictor          7

Training data contained 41 data points and no missing data.

Operations:

Centering for SO2, Temp, Empresas, Pob, Viento, Precip, Dias [trained]
Scaling for SO2, Temp, Empresas, Pob, Viento, Precip, Dias [trained]
PCA extraction with SO2, Temp, Empresas, Pob, Viento, Precip, Dias [trained]
pca_estimates %>% names()
[1] "var_info"       "term_info"      "steps"          "template"      
[5] "retained"       "tr_info"        "orig_lvls"      "last_term_info"

Nuestros resultados de los pasos de la receta de ACP están disponibles en steps. En nuestro caso usamos tres pasos, dos para normalizar los datos y uno para hacer ACP. Por lo tanto, el objeto steps es una lista de tamaño tres, donde los dos primeros elementos contienen detalles sobre nuestros pasos de normalización y el tercer elemento contiene los resultados de ACP. Revisemos el tercer paso.

pca_tidy <- pca_estimates$steps[[3]]
pca_tidy
$terms
<list_of<quosure>>

[[1]]
<quosure>
expr: ^all_numeric()
env:  0x7fb3b28d11c0


$role
[1] "predictor"

$trained
[1] TRUE

$num_comp
[1] 5

$threshold
[1] NA

$options
list()

$res
Standard deviations (1, .., p=7):
[1] 1.6517021 1.2297702 1.1810897 0.9444529 0.5888792 0.3166822 0.1597339

Rotation (n x k) = (7 x 7):
                   PC1         PC2        PC3         PC4        PC5
SO2       0.4896988171  0.08457563 -0.0143502  0.40421007  0.7303942
Temp     -0.3153706901 -0.08863789 -0.6771362 -0.18522794  0.1624652
Empresas  0.5411687028 -0.22588109 -0.2671591 -0.02627237 -0.1641011
Pob       0.4875881115 -0.28200380 -0.3448380 -0.11340377 -0.3491048
Viento    0.2498749284  0.05547149  0.3112655 -0.86190131  0.2682549
Precip    0.0001873122  0.62587937 -0.4920363 -0.18393719  0.1605988
Dias      0.2601790729  0.67796741  0.1095789  0.10976070 -0.4399698
                 PC6          PC7
SO2      -0.18334573 -0.149529278
Temp     -0.61066107  0.023664113
Empresas  0.04273352  0.745180920
Pob       0.08786327 -0.649125507
Viento   -0.15005378 -0.015765377
Precip    0.55357384  0.010315309
Dias     -0.50494668 -0.008217393

$prefix
[1] "PC"

$keep_original_cols
[1] FALSE

$skip
[1] FALSE

$id
[1] "pca_0gtrC"

attr(,"class")
[1] "step_pca" "step"

Vemos que las cargas de cada CP quedan guardadas en el argumento res. Si las comparamos con las obtenidas en princomp vemos que coinciden salvo signo de nuevo.

paste("TIDYMODELS")
[1] "TIDYMODELS"
pca_tidy$res$rotation %>% round(3)
            PC1    PC2    PC3    PC4    PC5    PC6    PC7
SO2       0.490  0.085 -0.014  0.404  0.730 -0.183 -0.150
Temp     -0.315 -0.089 -0.677 -0.185  0.162 -0.611  0.024
Empresas  0.541 -0.226 -0.267 -0.026 -0.164  0.043  0.745
Pob       0.488 -0.282 -0.345 -0.113 -0.349  0.088 -0.649
Viento    0.250  0.055  0.311 -0.862  0.268 -0.150 -0.016
Precip    0.000  0.626 -0.492 -0.184  0.161  0.554  0.010
Dias      0.260  0.678  0.110  0.110 -0.440 -0.505 -0.008
paste("PRINCOMP")
[1] "PRINCOMP"
pca$loadings

Loadings:
         Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
SO2       0.490                0.404  0.730  0.183  0.150
Temp     -0.315         0.677 -0.185  0.162  0.611       
Empresas  0.541 -0.226  0.267        -0.164        -0.745
Pob       0.488 -0.282  0.345 -0.113 -0.349         0.649
Viento    0.250        -0.311 -0.862  0.268  0.150       
Precip           0.626  0.492 -0.184  0.161 -0.554       
Dias      0.260  0.678 -0.110  0.110 -0.440  0.505       

               Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
SS loadings     1.000  1.000  1.000  1.000  1.000  1.000  1.000
Proportion Var  0.143  0.143  0.143  0.143  0.143  0.143  0.143
Cumulative Var  0.143  0.286  0.429  0.571  0.714  0.857  1.000

Accediendo al tercer elemento podemos obtener las desviaciones estándar del análisis de ACP y utilizarlas para calcular el porcentaje de variación explicado por cada CP. Para dar la varianza elevamos al cuadrado, que coinciden con los autovalores de \(\mathbf{\hat R}\).

sdev <- pca_estimates$steps[[3]]$res$sdev
percent_variation <- 100*sdev^2 / sum(sdev^2)
var_df <- tibble(CP = paste0("PC",1:length(sdev))) %>% 
  mutate(Var = sdev^2,
         Per_explained = percent_variation, 
         Cumulative_Per_Explained = cumsum(Per_explained))
var_df %>% kable()
CP Var Per_explained Cumulative_Per_Explained
PC1 2.7281197 38.9731383 38.97314
PC2 1.5123349 21.6047836 60.57792
PC3 1.3949730 19.9281856 80.50611
PC4 0.8919913 12.7427327 93.24884
PC5 0.3467787 4.9539809 98.20282
PC6 0.1002876 1.4326799 99.63550
PC7 0.0255149 0.3644989 100.00000

Ahora podemos construir el gráfico el scree plot que muestra y de forma similar el del porcentaje variabilidad explicada por cada CP.

var_df %>%
  mutate(CP = fct_inorder(CP)) %>%
  ggplot(aes(x = CP, y = Var)) +
  geom_bar(stat="identity",width=0.01) + 
  geom_point() +
  geom_hline(yintercept=1, linetype="dashed", color = "red") + 
  theme_pander()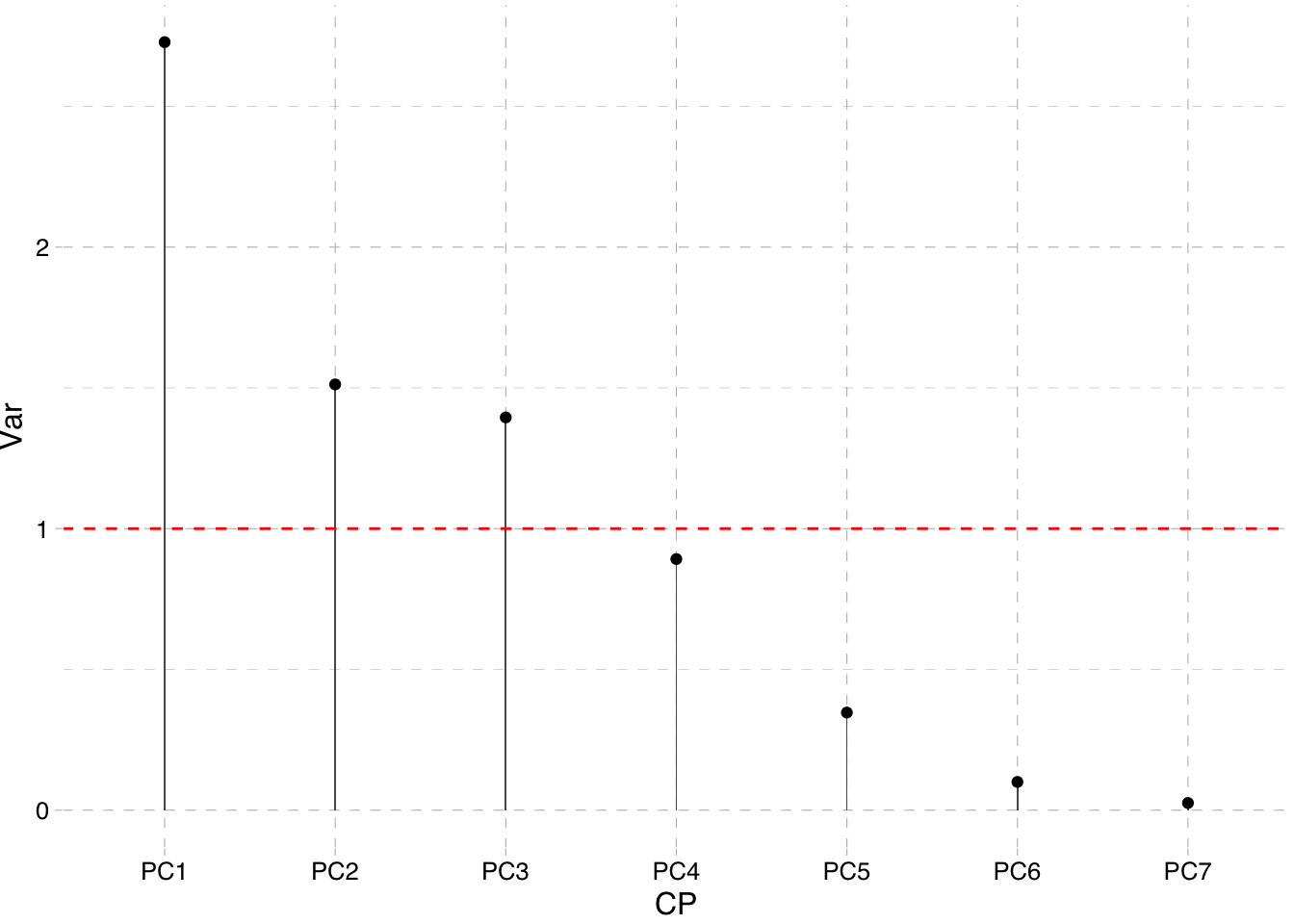 

var_df %>%
  mutate(CP = fct_inorder(CP)) %>%
  ggplot(aes(x = CP, y = Per_explained)) +
  geom_col(fill = "cornflowerblue", color = "red") + 
  ylab("Variablidad explicada") + theme_pander()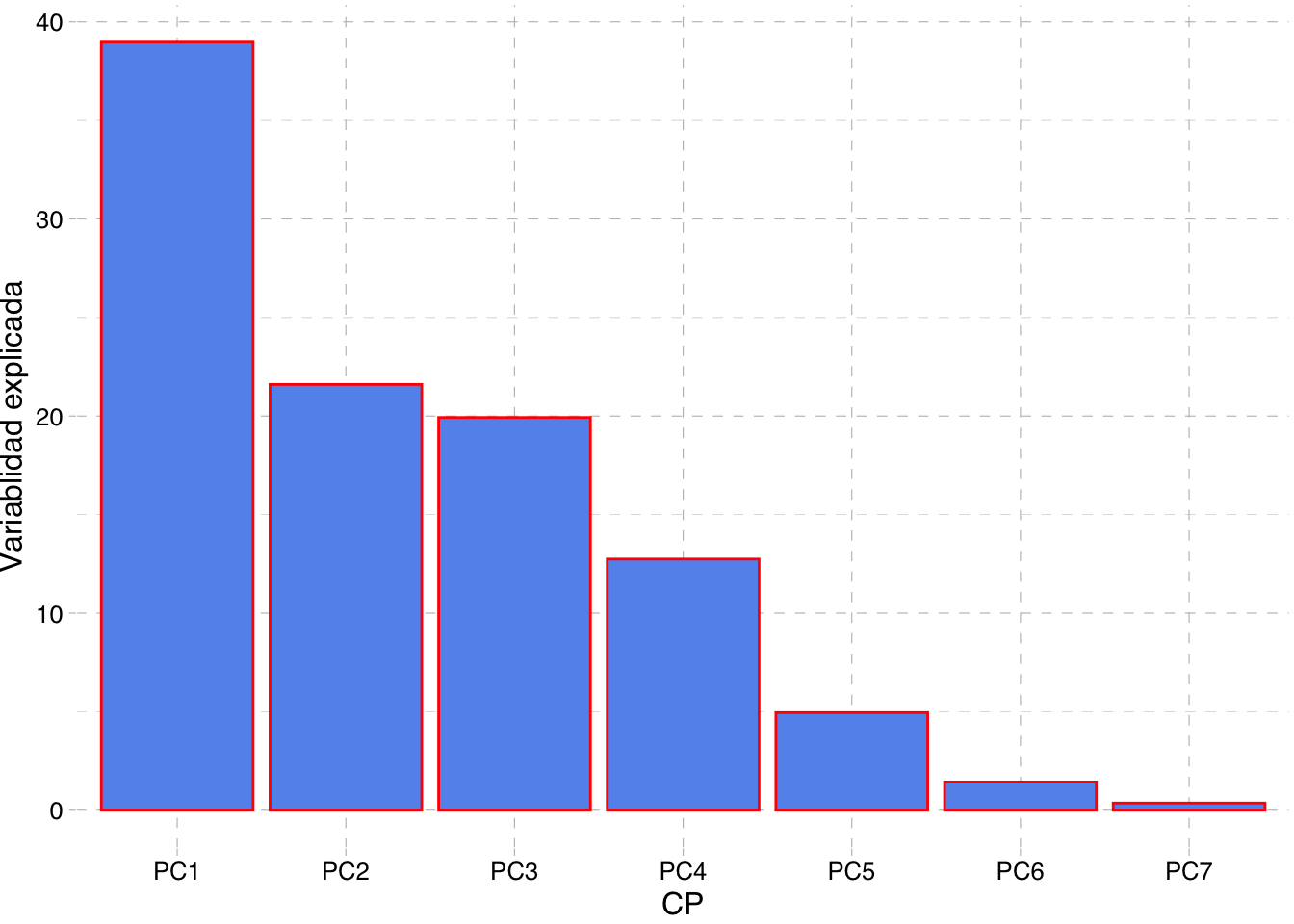

Echemos un vistazo a los componentes principales calculados por nuestra receta. El paquete de recipes de tidymodels tiene una función llamada juice, “jugo”, que devolverá los resultados de una receta creada por prep.

juice(pca_estimates) 
# A tibble: 41 x 5
       PC1     PC2    PC3     PC4     PC5
     <dbl>   <dbl>  <dbl>   <dbl>   <dbl>
 1 -2.68   -3.84   -1.05   1.52    0.0327
 2 -1.70    0.477  -0.840  0.192   0.140 
 3 -0.927  -2.21    0.181  0.151  -0.183 
 4 -0.543  -1.95    1.21   0.418  -0.379 
 5  0.455   1.08    0.582  0.927   0.734 
 6 -0.689   0.624   0.416  0.483   0.538 
 7 -0.0456 -0.0503 -0.350 -0.0435 -0.0290
 8 -1.36    0.927  -1.84  -0.449   0.0137
 9 -1.69    1.49   -2.55  -0.819   0.0562
10 -0.611   0.630  -0.976 -0.194   0.111 
# … with 31 more rows

Podemos usar los resultados de juice para hacer un diagrama de ACP estándar, un diagrama de dispersión con la CP1 en el eje \(x\) y la CP2 en el eje \(y\) para ver la estructura en los datos.

juice(pca_estimates) %>%
  ggplot(aes(PC1, PC2, label = rownames(aire.dat))) +
  geom_point(color="salmon", alpha = 0.7, size = 2,show.legend = FALSE) +
  geom_text(check_overlap = TRUE) + 
  labs(title="PCA with Tidymodels") + theme_pander()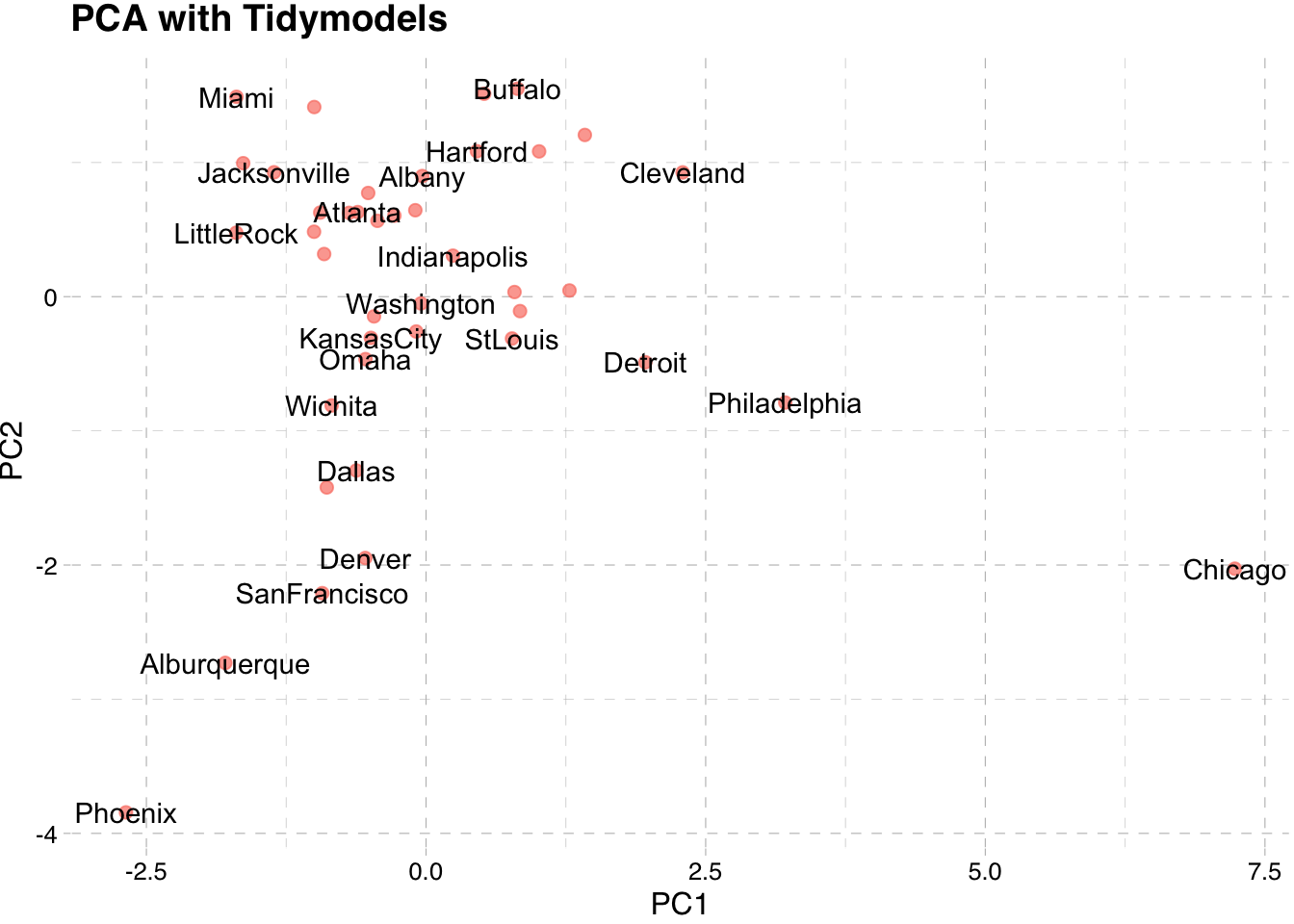

Obviamente el uso de tidymodels supone en ocasiones un mayor esfuerzo en cuanto a código se refiere y que sea una perspectiva novedosa también influye en su comprensión y manejabilidad. No obstante, se sigue un proceso estructurado lo que facilitará su entendimiento a largo plazo y, como se comentaba anteriormente, la comunidad lleva tiempo mostrando interés en metodologías como está que seguramente terminarán imperando en la minería de datos y programación estadística.

  1. ¿Por qué la interpretación es la misma aunque cambie el signo? El ACP proporciona vectores principales que apuntan en las mejores direcciones para proyectar sus datos en términos de varianza o error al cuadrado, ignorando el signo. Un vector principal que apunta en la dirección opuesta también es una solución válida para ACP pero le dará componentes principales con el signo opuesto. Informalmente, se puede decir que \(Variables \ originales \approx Cargas \times Puntuaciones\). Desde aquí podemos ver que si se cambia el signo de sus puntuaciones y de sus cargas, entonces esto no tendrá influencia en el resultado (o interpretación), porque \(-1\times-1 = 1\), idem si se cambia el de la CP y solo uno de las cargas o puntuaciones. Solo para proporcionar una mayor relevancia matemática, las direcciones en las que actúan los componentes principales corresponden a los autovectores del sistema. Si obtiene un CP positivo o negativo, solo significa que se está proyectando en un vector propio que apunta en un sentido ó \(180^\circ\) en el otro. Un autovector para una matriz (transformación lineal) \(A\) se define como cualquier vector \(v\neq0\) que satisfaga \(Av = \lambda v\). Si \(v\) es un autovector, cualquier múltiplo escalar \(\hat{v}=\alpha v\) también funcionará \((\alpha \neq 0)\): \[\begin{align} A v = \lambda v & \iff \alpha A v = \alpha \lambda v \\ & \iff A \hat v = \lambda \hat v \end{align}\] Esto incluye que se pueda eligir \(\alpha = -1\). Si \(v\) es un autovector, también lo es \(-v\). Digamos que el algoritmo ACP garantiza que \(\| v \|=1\). Todavía tienes dos posibilidades porque si tomas la intersección de una línea que pasa por el origen y el círculo unitario, obtienes dos puntos. La conclusión es que para cada componente de ACP, el signo de sus puntuaciones y de sus cargas es arbitrario. Además como se comentó en el desarrollo teórico las distancias se siguen manteniedo. Se puede modificar el signo de forma manual para adecuarlo a sus datos. En R, como se dice en la documentación de los signos de las columnas de las cargas y las puntuaciones son arbitrarios, por lo que pueden diferir entre diferentes programas para el ACP, e incluso entre diferentes compilaciones de R. Seguramente en el algoritmo programado el signo del autovector se elija de forma aleatoria y por eso puede cambiar al replicarse en otro momento. fix_sign = TRUE alivia eso.↩︎

>> Home